12.3. The Saga of the Eigenvalue Problem¶
A review of linear algebra literature from the beginning of the twentieth century until the 1970s shows that two problems were paramount to the researchers—systems of linear equations and the eigenvalue problem. The eigenvalue problem was an unsolved conundrum at the dawn of the twentieth century. However, two nineteenth-century mathematicians established important facts about the eigenvalue problem. French mathematician Augustin-Louis Cauchy (1789–1857) determined in 1827 that symmetric matrices would be the simplest type of matrix to diagonalize [1] [STEWART93]. He also established the criteria for two matrices having the same eigenvalues–now called similar matrices. German mathematician Carl Gustav Jacob Jacobi (1804–1851) proposed an iterative method in 1846 for calculating the eigenvalues and eigenvectors of real symmetric matrices [STRANG16]. His method used similarity transformations and rotation matrices similar to Givens rotations. Jacobi was also the first to note that converting a matrix to triangular form was sufficient for finding the eigenvalues as the eigenvalues are on the diagonal of triangular matrices (Eigenvalues of Triangular Matrices).
Progress in the first seventy years of the twentieth century was slow. Many promising algorithms failed to converge with certain matrices. Wilkinson’s extensive text [WILKINSON65] from 1965 is devoted to the sole topic of the eigenvalue problem. Wilkinson reviews several of the most promising algorithms from the late 1950s to the middle of the 1960s. He considered Each algorithm in terms of speed and robustness to converge, numerical accuracy and stability, and known problems. Wilkinson reviewed Francis’s QR algorithm and the LR algorithm, the previous top contender. But Francis’s algorithms were quite new. So Wilkinson holds back from declaring that Francis had won the prize. In this section, we will cover the individuals and developments that are known to have directly led to the QR algorithm and the Francis algorithm with implicit shifts.
Perhaps the first to demonstrate that solving the eigenvalue problem can be preferable to attempting to factor a polynomial was Perron in 1907 [PERRON07]. Perron was particularly interested in methods to find the eigenvalues of symmetric matrices. He established the theoretical foundation for the convergence of iterative eigenvalue algorithms. However, almost all publications on the topic of eigenvalues and factoring polynomials from before computers were available, suggest that the polynomial approach might be easier to solve. Opinions shifted toward the eigenvalue solution after computers became available because early computers could not accurately store the small numbers needed by polynomial solving algorithms [WATKINS11].
Schur’s 1909 article [SCHUR09] established orthogonal factoring methods as a strategy for solving the eigenvalue problem. However, given the lack of useful unitary transformation matrices the Schur triangularization theorem (Schur Triangularization Theorem in The Schur Decomposition) was rather theoretical at the time.
Müntz (1913) described the first eigenvalue algorithm [MUNTZ13] that could find a complex eigenvalue, although only one. He developed an early version of what we know today as the power method, which finds the eigenpair with the largest eigenvalue. The power method (The Power Method) is an important algorithm because some problems only need the first eigenpair, [2]. It is also a simple algorithm to understand and implement. The texts by Demmel [DEMMEL97] and Watkins [WATKINS10] describe the modern power method.
Turnbull and Aitken (Anticipation of Unitary Matrices) advocated in 1932 for and proved the existence of a unitary transformation matrix to rotate a column vector onto its first coordinate axis, which is what Householder later developed.
Horst (1937) may have developed the first procedure that could find all
of the eigenvalues and eigenvectors of a matrix
[HORST37]. However, the procedure is only applicable
to a special class of matrices. He was concerned with using an
eigenvalue algorithm to find the singular value decomposition using the
classic algorithm (The Classic SVD). Thus, he was interested in the
eigenpairs of a symmetric, positive definite matrix
(
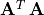). He described an algorithm similar to
the power method that finds the eigenpairs one at a time. Due to the
structure of the matrix, the procedure he describes, unlike the power
method, finds all of the eigenpairs.
Givens and Householder developed the two unitary matrices during the 1950s at Oak Ridge National Laboratory that was needed to solve the eigenvalue problem and, indeed, is the basis for other orthogonal factorizations. See Givens Rotation Matrices, Householder Reflection Matrices, The Origin of the Givens Rotation Transformation, and The Origin of the Householder Reflection Transformation.
Concurrent with Givens’ and Householder’s work on unitary matrices, Rutishauser developed the LR algorithm (The LR Algorithm), which completed the preliminary research needed to give Francis a foundation from which he was able to develop the QR algorithm.
| [1] | Diagonalize is another term for finding the eigendecomposition. |
| [2] | Google’s page rank algorithm is a prime example. |
