12.3.6. The LR Algorithm

During the 1950s, when Alston Householder and his colleagues in the Mathematics Division at Oak Ridge National Laboratory were first learning how to operate, maintain, and program a computer, Eduard Stiefel and his staff were going through the same learning experience at the Institute of Applied Mathematics at ETH Zurich, Switzerland. Stiefel hired Heinz Rutishauser to research numerical methods that could be programmed to run on a computer [GUTKNECHT10].

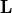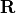Rutishauser developed what was called the qd algorithm [1] to find the roots of a particular type of polynomial. He observed that the work of the qd algorithm was the same as factoring a tridiagonal matrix into a product of lower and upper triangular matrices and then forming the product in reverse order. He called the two triangular matrices and . Thus, he proposed the LR algorithm based on the following similarity transform.

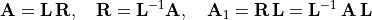
The LR algorithm was proposed as a method to find the eigenvalues of a matrix or the roots of a polynomial. Today, we would call his LR factoring the LU decomposition, which is solved with an elimination procedure (LU Decomposition). For numerical stability, LU decomposition requires pivoting, which complicates the algorithm.

Rutishauser’s LR algorithm was the inspirational strategy that led John Francis to the QR algorithm. Although LU decomposition uses elimination instead of orthogonal factoring methods, it still provides a way to find the eigenvalues of some matrices. Consider the following example where a close approximation to the eigenvalues of a 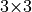positive definite matrix is found in MATLAB’s Command Window with ten iterations of the similarity transformation.

>> A = 5*randn(3);
>> A = A*A';
>> eig(A)
ans =
    0.1294
    9.9568
   44.5828
>> for i=1:10
[L,U] = lu(A);
A = U*L;
end
>> sort(diag(A))
ans =
    0.1294
    9.9567
   44.5829

[1]	Abbreviation qd stands for quotient-difference.