12.3.5. Oak Ridge and Unitary Matrices

Wallace Givens and Alston Householder developed the Givens rotation transform and the Householder reflection transform during the 1950s at Oak Ridge National Laboratory [1] (ORNL) in Oak Ridge, Tennessee. The set of technologies that researchers at ORNL study include mathematics and computing. Alston Householder became the head of a new department called the Mathematics Panel in 1948. Householder attended the unveiling of the Mark I at Harvard and became convinced that Oak Ridge needed a large computing facility. After receiving bids from several vendors, ORNL purchased a copy of the Institute for Advanced Study (IAS) machine that John von Neumann designed. They gave their computer the name ORACLE, which was an acronym for Oak Ridge Automatic Computer and Logical Engine. It was built at Argonne National Laboratory and installed at ORNL in February 1954 [MERTZ70].

What ORNL had in ORACLE, and IBM machines that later replaced it, was a machine that required a staff of engineers to maintain and operate it. The facilities for input/output and programming were limited. The Annual Progress Reports of the Mathematics Panel [2] for the 1950s and 1960s document the progression of developing a library of essential programming functions, including mathematical functions. They wrote ORACLE’s early programs in assembly language. The programming capabilities improved considerably after they developed a compiler for the ALGOL programming language.

The Mathematics Panel worked on and wrote computer programs to solve problems in several branches of mathematics. Householder himself and a few other researchers, including Wallace Givens, had a strong interest in linear algebra and numerical analysis. Their highest priorities included unitary matrices, algorithms for orthogonal matrix factoring, and the eigenvalue problem.

12.3.5.1. The Origin of the Givens Rotation Transformation

Since geometric rotation matrices were known to be orthogonal, the strategy of using multiplication with a unitary matrix to change a matrix element to zero using rotation about another matrix element as described in Givens Rotation Matrices appears to have been a fairly obvious starting point for Alston Householder and Wallace Givens. Jacobi successfully used similar rotations more than one hundred years earlier to find the eigenvalues of the simplest matrix type (real and symmetric). Householder reports in his 1953 text [HOUSEHOLDER53] that Givens wrote about the construction of the rotation transformations in an ORNL internal memorandum in 1951. It is unknown to what extent Householder was involved in Givens’ work. He would have certainly been an advisor since Givens then reported to Householder.

Who was Wallace Givens?

James Wallace Givens Jr. (1910–1993) received his Ph.D. in mathematics from Princeton University in 1936. After graduation, he worked with the UNIVAC computer at NYU , one of the first stored program control computers. He next went to ORNL and worked with Alston Householder in the Mathematics Panel. He held faculty teaching positions at the University of Tennessee, Wayne State University, and Northwestern University. He served as the director of the Division of Applied Mathematics at Argonne National Laboratories from 1964 to 1970. He served as the president of the Society of Industrial and Applied Mathematics from 1968 to 1970. He retired in 1979 from Northwestern University.

Beyond just developing the unitary transformation, Given developed programs to apply it to numerical analysis problems. He authored an ORNL Technical Report in March of 1954 on using unitary rotations to calculate the eigenvalues of symmetric matrices [GIVENS54]. Then, he reported in the December 1954 Semiannual Progress Report for the Mathematics Panel that he could also find the eigenvectors of symmetric matrices [ORNL54]. In the Semiannual Progress Report of June 1956, he reported using unitary rotations to find the inverse of a matrix. However, he also reported only partial success in finding the eigenvalues of non-symmetric matrices [ORNL56].

After leaving ORNL for a faculty position at Wayne State University, Givens published a paper describing difficulties associated with the eigenvalue problem for non-symmetric matrices [GIVENS57]. This report does not go into the same level of detail about the algorithms he used as the technical report he wrote at ORNL. He presented a paper at a conference in late 1957 that was later published as a full JACM journal article in 1958 giving more details about unitary rotations and their application to the eigenvalue problem [GIVENS58]. This is the most frequently cited article for Givens rotation transformations.

12.3.5.2. The Origin of the Householder Reflection Transformation

Owing likely to the humility of Dr. Householder, reflection transformations were introduced with minimal publicity. The paper in which they were introduced [HOUSEHOLDER58] is only slightly over three pages long, and the only suggested application is for QR factoring to solve systems of equations or to calculate the inverse of a matrix. The given reason for developing the unnamed transform is to provide an alternative to Givens rotators for some applications. He points out that 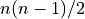rotators, each with a computationally expensive square root, are required for a 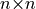QR factorization. The Householder transform only needs 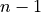transforms to accomplish the same task. Householder transforms are also faster on integer processors because they do not require square root calculations. He also briefly described the transformation in his 1964 book on numerical analysis [HOUSEHOLDER64].

Who was Alston Householder?

Alston Scott Householder (1904–1993) received his B.S. degree from Northwestern University in 1925, his M.A. degree from Cornell University in 1927, and his Ph.D. degree the University of Chicago in 1937. He was also given an honorary doctorate from the Munich Technological Institute in 1965. His early research efforts were related to mathematical biology. He then taught at several universities. After serving as a consulting mathematician at the Naval Research Laboratory during WWII, he switched his research interests to numerical analysis at Oak Ridge National Laboratory. He was a senior mathematician and director of the ORNL Mathematics Division from 1946 to 1969. He then became a professor of mathematics at the University of Tennessee until he retired in 1974 [OCONNOR99].

He is most remembered for the Householder transform, but he also pioneered the systematic use of norms in linear algebra [CIARLET94]. He was highly regarded for his administrative leadership. He was a significant influence and mentor to countless other researchers as the head of mathematics research at ORNL. He was a founding editor of Numerische Mathematik in 1959. He organized and hosted the annual Gatlinburg Symposium on Numerical Linear Algebra, where numerical analysts worldwide gathered to share their latest research results.

He authored many conference papers and journal articles. He wrote three books—[HOUSEHOLDER53], [HOUSEHOLDER64], and [HOUSEHOLDER70]. In the Preface to his last book [HOUSEHOLDER70], he wrote that his three books all represent an effort to organize and expound principles developed largely by pure mathematicians that might be useful to the numerical analyst. Householder described himself as having the training of a pure mathematician but was excited about applying mathematics to real problems. He was particularly interested in numerical analysis and the ability of computers to execute iterative algorithms to solve problems that can not be solved analytically. Householder is described as having a love for teaching and being a mentor [STEWART79].

It is now widely accepted that the Householder reflector is perhaps the most useful tool available in numerical analysis [DUBRULLE00]. The Givens rotator certainly has applications, but the Householder transform provides the foundation for orthogonal matrix factoring. Householder mentioned applying it to the QR decomposition, but it now has a role in every orthogonal matrix factorization.

Householder does not refer to the transform as a reflection matrix. Others gave it that name. The general equation for a reflection was known, but Householder adjusted the application. A reflection problem is often viewed from the perspective of finding the reflection of a vector relative to a fixed hyperplane, such as a mirror [HIGHAM02]. In the Householder transform equation, we know what the vector is and the target of where it should reflect. The location of the reflective hyperplane is found in the form of its normal vector (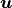 in equation (12.2)). Then the reflector matrix is found from .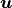

Householder also does not say how he developed the reflection equation. Turnbull and Aitken wrote about the need and existence of such a transformation some 25 years previously [TURNBULL32]. Turnbull and Aitken referred to it as a type of rotation, which it is, but we already have Givens rotators, so we don’t use that moniker. Anyone with knowledge of linear algebra would naturally think about using projection equations to find the reflector matrix after examining figure Fig. 12.3. However, he does not mention vector projections in his publications.

[1]

After the conclusion of the Manhattan Project and World War II, the laboratory at Oak Ridge took on the task of developing nuclear reactor technology for the U.S. Department of Energy in 1943. The laboratory still operates as a research institution. As their website (https://www.ornl.gov/) states, “Oak Ridge National Laboratory delivers scientific discoveries and technical breakthroughs needed to realize solutions in energy and national security and provide economic benefit to the nation.”

[2]

Scanned copies of these reports are available on the website of the Department of Energy’s Office of Scientific and Technical Information (https://www.osti.gov/).