12.3.1. Eigenvalues of Triangular MatricesΒΆ

Although we do not generally use the determinant of the characteristic equation to find eigenvalues, considering the determinant does give us an insight into the quickest procedure for finding the eigenvalues. Because of the zeros in a triangular matrix, its determinant is the product of the elements on the diagonal. Likewise, the determinant of a triangular characteristic equation reveals the product of the characteristic factors. As first observed by Jacobi, [1] the eigenvalues may be taken directly from the diagonal values of diagonal, upper triangular, and lower triangular matrices.

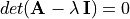
det(\mathbf{A} - \lambda\,\mathbf{I}) = 0

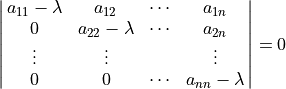
\spaligndelims\vert\vert \spalignmat{{a_{11} - \lambda} a_{12} {\cdots} a_{1n}; 0 {a_{22} - \lambda} {\cdots} a_{2n}; {\vdots} {\vdots} {} {\vdots}; 0 0 {\cdots} {a_{nn} - \lambda}} = 0

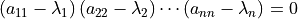
(a_{11} - \lambda_1)\,(a_{22} - \lambda_2)\cdots (a_{nn} - \lambda_n) = 0

[1]The upper triangular form of a matrix is sometimes referred to as the Jacobi canonical form. Although, that moniker is less common in current literature than it once was.