12.3.4. Anticipation of Unitary Matrices¶
Chapter VIII of Herbert Turnbull and Alexander Aitken’s 1932 text [TURNBULL32] discusses the utility of unitary transformation matrices. Section 2 covers the topic of vector rotations from multiplication by a unitary matrix. They prove the existence of a unitary matrix that matches what we now call a Householder reflection matrix. They begin with a lemma and its proof for using a unitary transformation to rotate a vector to another vector of the same length.
Lemma 12.1
Any two non-zero vectors of orderhaving equal norms may be transformed into each other by unitary transformations. For vectors
and
if
, then there exists a unitary matrix
such that
.
They extend the lemma to establish the existence of the Householder reflection transform.
Theorem 12.4
A unitary matrixexists, which transforms a given vector of norm
into {
}.
We recognize 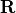 as an early form of Householder reflection
because the resulting vector contains only zero elements in positions
other than the first. Turnbull and Aitken do not give an algorithm for
finding
as an early form of Householder reflection
because the resulting vector contains only zero elements in positions
other than the first. Turnbull and Aitken do not give an algorithm for
finding 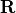 .
.
Turnbull and Aitken project an application of the transform to the Schur decomposition. The form of the Schur decomposition [SCHUR09] was already established when Turnbull and Aitken wrote, although it was not yet so named. They give a theorem that restates the Schur triangularization theorem and proves that a transform such as what Householder later developed meets the unitary requirements of Schur Triangularization Theorem.
They further prove that if 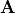 is Hermitian, then the
reduction to upper triangular form yields a diagonal matrix of the
eigenvalues and that the columns of
is Hermitian, then the
reduction to upper triangular form yields a diagonal matrix of the
eigenvalues and that the columns of 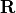 are the
eigenvectors of
are the
eigenvectors of 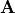 . (See The Schur Decomposition of Symmetric Matrices.)
. (See The Schur Decomposition of Symmetric Matrices.)
Although Turnbull and Aitken establish the existence of the modern Householder reflection transformation and its utility in finding the Schur decomposition, they do not show algorithms for finding either. That must wait for future generations of mathematicians and for computers to run the algorithms.
