10. Principal Component Analysis (PCA)

As the name implies, Principal Component Analysis (PCA) accentuates the principal components of data such that the salient features of the data are more apparent. Like the SVD, PCA reduces the dimensionality of data, emphasizing the distinguishing characteristics while removing the insignificant. The PCA algorithm maps the data into a new vector space called the PCA space. From the PCA space, the data may be reconstructed with reduced dimension. However, using the PCA space data for classification and recognition applications is more common. In the PCA space, similar items are grouped together and separated from clusters of dissimilar items.

PCA can help automate the classification of items based on measurable features. PCA uses correlations between the features to find a linear combination of the features such that similar items are clustered together in the PCA space. PCA uses the most significant eigenvectors from a covariance matrix to find the linear combinations of the features. Using a covariance matrix is significant to PCA as it reveals how similar and dissimilar (at variance) the data samples are. Then, when we multiply sample data by the most significant eigenvectors (determined by the eigenvalues), the differences and similarities between the items become more obvious.

The data can be arranged in a matrix with \(n\) measured features from \(m\) sources (samples). Examples of potential data sets include the stock values from \(m\) companies taken over \(n\) days, opinions of \(m\) customers regarding \(n\) competing products, or the grades of \(m\) students in \(n\) courses. In the examples presented here, the matrix columns hold the measured features, and each row holds the data from one source. However, with adjustments to the equations, the data may be transposed with the features in rows and the samples in columns.

To make a covariance matrix, we first subtract the mean of each feature from the data so that each feature has a zero mean.

\[\begin{split}\mathbf{D} = \begin{bmatrix} \vertbar{} & \vertbar{} & {} & \vertbar{} \\ (\bm{x}_1-\mu_1){} & (\bm{x}_2-\mu_2){} & \cdots{} & (\bm{x}_n-\mu_n){} \\ \vertbar{} & \vertbar{} & {} & \vertbar{} \end{bmatrix}\end{split}\]

Recall from Covariance and Correlation that a covariance matrix is symmetric with the variance of each feature on the diagonal and the covariance between features in the off-diagonal positions.

\[\mathbf{Cov_x} = \frac{\mathbf{D}^T\,\mathbf{D}}{m - 1}\]

\[\begin{split}\mathbf{Cov_x} = \begin{bmatrix} Var({x_1, x_1}) & Cov({x_1, x_2}) & \cdots & Cov({x_1, x_n}) \\ Cov({x_2, x_1}) & Var({x_2, x_2}) & \cdots & Cov({x_2, x_n}) \\ \vdots & \vdots & \ddots & \vdots \\ Cov({x_n, x_1}) & Cov({x_n, x_2}) & \cdots & Var({x_n, x_n}) \end{bmatrix}\end{split}\]

Next, the eigenvectors, \(\mathbf{V}\), and eigenvalues of the covariance matrix are found. The eigenvalues are used to sort the eigenvectors. Because we wish to achieve dimensionality reduction, only the eigenvectors corresponding to the \(k\) largest eigenvalues are used to map the data onto the PCA space.

\[\mathbf{W} = \begin{bmatrix} \bm{v}_1 & \cdots & \bm{v}_k \end{bmatrix}\]

\(\bf{W}\) gives us the basis vectors of the PCA space. Multiply each sample vector by the \(\bf{W}\) matrix to project the data onto the PCA space.

\[\mathbf{Y} = \mathbf{D\,W}.\]

We display or compare the data in the PCA space (\(\bf{Y}\)) for classification and object recognition purposes.

Reverse the steps to reconstruct the original data with reduced dimensionality.

\[\begin{split}\begin{array}{ll} \mathbf{\tilde{X}} &= \mathbf{D} + \bm{\mu} \\ &= \mathbf{W\,(W}^T\,\mathbf{D}) + \bm{\mu} \\ &= \mathbf{W\,Y} + \bm{\mu} \end{array}\end{split}\]

Transposed data

If the measured features are held in the rows and the samples are in the columns, then the adjusted equations are as follows.

\[\begin{split}\mathbf{D} = \begin{bmatrix} \horzbar{} & {(\bm{x}_1 - \mu_1)}\horzbar{} \\ \horzbar{} & {(\bm{x}_2 - \mu_2)} & \horzbar{} \\ \vdots{} & \vdots{} & \vdots{} \\ \horzbar{} & {(\bm{x}_n - \mu_n)} & \horzbar{} \end{bmatrix}\end{split}\]

\[\mathbf{Cov_x} = \frac{\mathbf{D\,D}^T}{n - 1}.\]

\[\mathbf{Y} = \mathbf{W}^T\mathbf{D}.\]

10.1. PCA for Data Analysis

To illustrate what PCA does with a simple plot, the PCA_demo script is an example of PCA with only two data features. Noise was added to the data to show how dimensionality reduction separates the correlated data from the uncorrelated noise. In this example, the data was reconstructed with reduced dimensionality. Notice the lines in figure Fig. 10.1 showing the principal and minor axes. The orientation of the principal axis is aligned with the correlation of the data, while the minor axis is aligned with the uncorrelated noise. Thus, as we also saw in Dimensionality Reduction for the SVD, the lower rank data is preferred to the full rank data that contains noise. Figure Fig. 10.1 shows a plot demonstrating that the reconstructed data is aligned with the correlation between the columns of the original data.

% File: PCA_demo.m
% PCA - 2D Example
n = 2; m = 50; X = zeros(m, n);
% two random but correlated columns
X(:,1) = 5*randn(m, 1) - 2.5;
X(:,2) = -1 + 1.5 * X(:,1) + 5*randn(m,1);
X = sortrows(X,1);

%% find PCA from eigenvectors of covariance
mu = mean(X);
D = X - repmat(mu, m, 1);
covx = D'*D/(m - 1);      % sources in rows, features in columns
[V, S] = eig_decomp(covx);
% project onto PCA space
W = V(:,1);
Y = D * W; % only use the dominant eigenvector
disp('Eigenvalue ratios to total'), disp(S/trace(S))
% Data reconstruction
Xtilde = Y*W' + repmat(mu, m, 1);
% plots
figure, scatter(X(:,1), X(:,2)), title('PCA Demo');
hold on
plot([0 5*V(1,1)], [0 5*V(2,1)]);  % principal axis
plot([0 5*V(1,2)], [0 5* V(2,2)]); % minor axis
plot(Xtilde(:,1), Xtilde(:,2));    % principal component
legend({'data in', 'principal axis', 'minor axis', ...
    'reconstruction'}, 'Location', 'northwest');
hold off

function [eigvec,eigval]=eig_decomp(C)
    [eigvec,eigval]=eig(C);
    eigval=abs(diag(eigval)');
    [eigval, order]=sort(eigval, 'descend');
    eigval=diag(eigval);
    eigvec=eigvec(:, order);
end

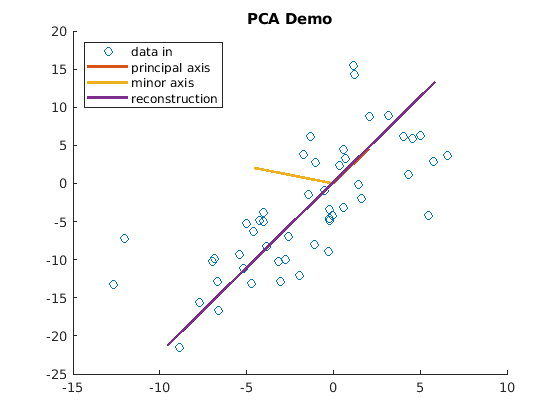
Fig. 10.1 The principal component of the reconstructed data from PCA is aligned with the correlation between the columns of the original data.

Is PCA the same as least squares regression?

The plot in figure Fig. 10.1 makes it appear that the reconstructed data from PCA is the same data fit as achieved from least squares regression; however, it differs in two ways.

1. In least squares regression, the minimized error is parallel to the \(y\) axis; whereas, in PCA, the minimized error is orthogonal to the data projection line (principal axis).

2. In least squares regression, the data fit is an extension of solving a system of linear equations for over-determined systems. In PCA, the data fit is a by-product of dimensionality reduction.

10.2. PCA for Classification

An important application of PCA is classification, which reduces the dimensions of the data, making it easier to see how the attributes of items of the same type are similar and differ from items of other types. In this example, we will look at a public domain dataset and produce a scatter plot showing how similar data are clustered in the PCA space.

The public domain data is in a file named nndb_flat.csv, which is part of the downloadable files from Canvas. The file can also be downloaded from the Data World website. [1] The data comes from the USDA National Nutrient Database and was made available by Craig Kelly. It lists many foods and identifies food groups, nutrition, and vitamin data for each. We will use the nutrition information in the analysis. The PCA_food script implements the PCA algorithm. The scatter plot in figure Fig. 10.2 shows the first two principal components for 8,618 foods in seven groupings. The plot shows clusters of foods by their groups and which food groups are nutritionally similar or different.

Fig. 10.2 Scatter plot of the first two principal components from nutrition data for 8,618 foods from seven food groups.

To see a list of all food groups in the data set, type the following in the command window after the FoodGroups variable is created by the script.

>> categories(FoodGroups)

Download the dataset and my MATLAB script.

nndb_flat.csv

PCA_food.m

10.3. PCA for Recognition

A fun example of how PCA can be used is for face recognition. The eigenvectors found from PCA give us a matrix for multiplying images of people’s faces. The PCA space data gives a more succinct representation of who is pictured in each image. The Euclidean distances between the images in the PCA space are calculated to find the most likely match of who is in each picture. An example implementation with quite accurate results is found on the MathWorks File Exchange web site [ALSAQRE19].

Recommended Additional Reading

Alaa Tharwat wrote a very good tutorial on PCA and posted it on MathWorks File Exchange [THARWAT16]. The tutorial presents both the SVD and covariance PCA algorithms.

Homework

Now complete PCA Data Classification homework.

Footnote:

[1]

https://data.world/