6.11.2. Projections Onto a Hyperplane¶
We can extend projections to \(\mathbb{R}^3\) and still visualize the projection as projecting a vector onto a plane. Here, the column space of matrix \(\bf{A}\) is two 3-dimension vectors, \(\bm{a}_1\) and \(\bm{a}_2\).
The span of two vectors in \(\mathbb{R}^3\) forms a plane. As before, we have an approximation solution to \(\mathbf{A}\,\bm{x} = \bm{b}\), which can be written as \(\mathbf{A}\,\bm{\hat{x}} = \bm{p}\). The error is \(\bm{e} = \bm{b} - \bm{p} = \bm{b} - \mathbf{A}\,\bm{\hat{x}}\). We want to find \(\bm{\hat{x}}\) such that \(\bm{b} - \mathbf{A}\,\bm{\hat{x}}\) is orthogonal to the plane, so again we set the dot products equal to zero.
The left matrix is just \(\mathbf{A}^T\), which is size \(2{\times}3\). The size of \(\bm{\hat{x}}\) is \(2{\times}1\), so the size of \(\mathbf{A}\,\bm{\hat{x}}\), like \(\bm{b}\), is \(3{\times}1\).
The orthogonal solution makes use of QR decomposition. Because \(\bf{A}\) is over-determined, the last \(m - n\) rows of \(\bf{R}\) will be all zeros, so we can reduce the size of \(\bf{Q}\) and \(\bf{R}\) with the economy QR option where only the first \(n\) columns of \(\bf{Q}\) are returned. \(\bf{Q}\) is now \(m{\times}n\), and \(\bf{R}\) is \(n{\times}n\). After finding \(\bf{Q}\) and \(\bf{R}\), computing the solution only requires one \(n{\times}m\) multiplication with a \(m{\times}1\) vector and then a \(n{\times}n\) back-substitution of an upper triangular matrix.
In MATLAB, we can find \(\hat{\bm{x}}\) as:
x_hat = (A'*A) \ (A'*b);
% or
[Q, R] = qr(A, 0); % Economy QR
x_hat = R \ (Q'*b);
Note
(A \ b) finds the same answer. The left-divide operator handles
under-determined, over-determined, and square matrix systems
Left-Divide Operator).
The projection vector is then:
The projection matrix is:
Note
\(\bf{A}\) is not a square matrix and thus is not invertible. If it were, \(\mathbf{P} = \bf{I}\) and there would be no need to do the projection. Try to verify why this is the case. Recall that \((\mathbf{BA})^{-1} = \mathbf{A}^{-1}\mathbf{B}^{-1}\).
6.11.2.1. Over-determined Pseudo-inverse¶
Recall from our discussion of square matrices that while we might write the solution to \(\mathbf{A}\,\bm{x} = \bm{b}\) as \(\bm{x} = \mathbf{A}^{-1}\,\bm{b}\), that is not how we should compute \(\bm{x}\) because computing the matrix inverse is slow. However, a one-time calculation of the LU decomposition of \(\bf{A}\) allows for convenient reuse of \(\bf{L}\) and \(\bf{U}\) when we compute multiple solutions with a fixed \(\bf{A}\) matrix and different \(\bm{b}\)’s. Similarly, sometimes we need a one-time calculation on rectangular systems that we can reuse as needed. This is the Moore–Penrose pseudo-inverse of \(\bf{A}\), which we denote as \(\bf{A}^+\), and \(\bm{x} = \mathbf{A}^+\,\bm{b}\) is the minimum length least squares solution to \(\mathbf{A}\,\bm{x} = \bm{b}\).
We have already found from projections that equation (6.28) is the least squares solution, but it has unacceptable computational performance.
If \(\bf{A}\) is not too large, then the MATLAB expression
x = (A’*A) \ (A’*b) is reasonable because
\(\left(\mathbf{A}^{T}\mathbf{A}\right)\) is positive definite and
the Cholesky solver can be used. However, we should avoid both the
matrix multiplication and the inverse matrix calculation of equation
(6.28), especially if \(\bf{A}\) is large. Strategies
based on orthogonal matrix factorizations are preferred.
Several matrix multiplications simplify to the identity matrix if we let \(\mathbf{A} = \mathbf{Q\, R}\) or \(\mathbf{A} = \mathbf{U\,\Sigma\,V}^T\) in equation (6.28).
The solutions based on QR and SVD in equation (6.29) are equivalent since computing the inverse of \(\bf{R}\) results in an SVD calculation. Matrices \(\bf{A}\) and \(\bf{R}\) are orthogonally equivalent, meaning they have the same singular values.
MATLAB uses the SVD to calculate the pseudo-inverses of both
over-determined system and under-determined systems The Preferred Under-determined Solution).
The MATLAB function is called as Aplus = pinv(A).
Since \(\bf{\Sigma}\) is a diagonal matrix, its inverse is the reciprocal of the nonzero elements on the diagonal. The zero elements remain zero.
>> S = diag([2 3 0])
S =
2 0 0
0 3 0
0 0 0
>> pinv(S)
ans =
0.5000 0 0
0 0.3333 0
0 0 0
Here is an example of using the pseudo-inverse on an over-determined matrix equation.
>> A=randi(20,15,4)-8;
>> y=randi(10,4,1)-4
y =
4
-1
2
3
>> b = A*y;
>> [U, S, V] = svd(A);
>> pinvA=V*pinv(S)*U';
>> x = pinvA*b
x =
4.0000
-1.0000
2.0000
3.0000
>> x = pinv(A)*b
x =
4.0000
-1.0000
2.0000
3.0000
6.11.2.2. Projection Example¶
The projectR3 script and the resulting plot in figure
Fig. 6.27 demonstrate the calculation and display
of a vector’s projection onto the matrix’s column space. The dot product
is also calculated to verify orthogonality.
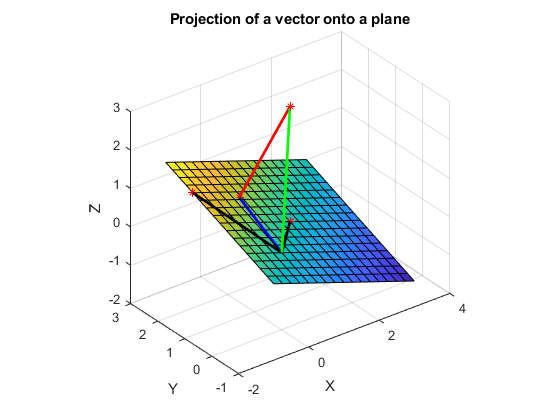
Fig. 6.27 The projection of a vector onto the column space of \(\bf{A}\), which spans a plane in \(\mathbb{R}^3\)¶
Two vectors, \(\bm{a}_1\) and \(\bm{a}_2\) define a plane. To find the equation for a plane, we first determine a vector, \(\bm{n}\), which is orthogonal to both vectors. The cross product provides this. The vector \(\bm{n}\) is defined as \(\bm{n} = [a\: b\: c]^T\). Then, given one point on the plane \((x_0, y_0, z_0)\), we can calculate the equation for the plane.
In this case, we know that the point \((0, 0, 0)\) is on the plane, so the plane equation is simplified.
The points of the plane are determined by first defining a region for
\(x\) and \(y\), then using the plane equation to calculate the
corresponding points for \(z\). A simple helper function called
vector3 was used to plot the vectors. A plot of the projection is
shown in figure Fig. 6.27.
% File: projectR3.m
% Projection of the vector B onto the column space of A.
% Note that with three sample points, we can visualize
% the projection in R^3.
%% Find the projection
% Define the column space of A, which forms a plane in R^3.
a1 = [1 1 0]'; % vector from (0, 0, 0) to (1, 1, 0).
a2 = [-1 2 1]';
A = [a1 a2];
b = [1 1 3]';
x_hat = (A'*A)\(A'*b);
p = A*x_hat; % projection vector
e = b - p; % error vector
fprintf('Error is orthogonal to the plane if close to zero:
%f/n', p'*e);
%% Plot the projection
% To make the equation for a plane, we need n, which is
% orthogonal normal vector to the column space, found from
% the cross product.
n = cross(a1,a2);
% Plane is: a(x-x0) +b(y-y0) + c(z-z0) + d = 0
% Variables a, b, and c come from the normal vector.
% Keep it simple and use point (0, 0, 0) as the point on
% the plane (x0, y0, z0).
a=n(1); bp=n(2); c=n(3); d=0;
[x, y] = meshgrid(-1:0.25:3); % Generate x and y data
z = -1/c*(a*x + bp*y + d); % Generate z data
figure;
surf(x,y,z); % Plot the plane
daspect([1 1 1]); % consistent aspect ratio
hold on;
z0 = [0 0 0]'; % vector starting point
vector3(z0, a1, 'k'); % column 1 of A
vector3(z0, a2, 'k'); % column 2 of A
vector3(z0, b, 'g'); % target vector
vector3(z0, p, 'b'); % projection
vector3(p, b, 'r'); % error from p to b
hold off;
xlabel('X');
ylabel('Y');
zlabel('Z');
title('Projection of a vector onto a plane');
% helper function
function vector3( v1, v2, clr )
% VECTOR3 Plot a vector from v1 to v2 in R^3.
plot3([v1(1) v2(1)], [v1(2) v2(2)], ...
[v1(3) v2(3)], 'Color', clr,'LineWidth',2);
end
6.11.2.3. Alternate Projection Equation¶
Not all linear algebra textbooks present the same equations for projecting a vector onto a vector space. The approach that we have used might be described as projecting a vector onto the column space of a matrix. An alternate approach projects a vector onto an equivalent vector space spanned by an orthonormal set of basis vectors. So the first step in the alternate approach is to find the orthonormal basis vectors of the matrix columns. (See Vector Spaces for help with some of the terminology.)
Let \(\mathbf{U} = \{ \bm{u}_1, \bm{u}_2, \ldots , \bm{u}_n \}\) be an orthonormal basis for the column space of matrix \(\bf{A}\). Then the projection of vector \(\bm{b}\) onto \(\text{Col}( \mathbf{A} )\) is defined by
There is a trade-off between the two algorithms. The alternative
approach finds the orthonormal basis vectors to the columns of
\(\bf{A}\) using either the Gram–Schmidt process
(Finding Orthogonal Basis Vectors), QR factorization (QR Decomposition), or the economy SVD
method (Projection and the Economy SVD), which is used by the orth function.
Whereas, projecting onto the column space requires solving an
\(\mathbf{A}\,\bm{x} = \bm{b}\) problem.
The geometry of the alternate algorithm provides a simple way to see that it also projects a vector onto a vector space.
Any vector in the vector space must be a linear combination of the orthonormal basis vectors.
The \(\bm{b}^T \bm{u}_i\) coefficients in the sum are scalars from the dot products of \(\bm{b}\) and each basis vector. Since the basis vectors are of unit length, each term in the sum is \(\left(\norm{\bm{b}}\,\cos(\theta_i)\right)\,\bm{u}_i\), where \(\theta_i\) is the angle between \(\bm{b}\) and the basis vector. Thus, each term in the sum is the projection of \(\bm{b}\) onto a basis vector.
The example in altProject script finds the projection using the two
methods. The mod_gram_schmidt function from Implementation of Modified Gram–Schmidt is used
to find the orthogonal basis vectors.
% File: alt_project.m
%% Comparison of two projection equations
% Define the column space of A, which forms a plane in R^3.
a1 = [1 1 0]'; % vector from (0, 0, 0) to (1, 1, 0).
a2 = [-1 2 1]';
A = [a1 a2];
b = [1 1 3]';
%% Projection onto the column space of matrix A.
x_hat = (A'*A)\(A'*b);
p = A*x_hat; % projection vector
disp('Projection onto column space: ')
disp(p)
%% Alternate projection
% The projection is the vector sum of projections onto
% the orthonormal basis vectors of the column space of A.
[U, ~] = mod_gram_schmidt(A); % Could use the orth function
u1 = U(:,1);
u2 = U(:,2);
p_alt = b'*u1*u1 + b'*u2*u2;
disp('Projection onto basis vectors: ')
disp(p_alt)
The output from the vector projection example follows.
>> alt_project
Projection onto column space:
0.1818
1.8182
0.5455
Projection onto basis vectors:
0.1818
1.8182
0.5455
6.11.2.4. Higher Dimension Projection¶
If the matrix \(\bf{A}\) is larger than \(3{\times}2\), then we can not visually plot a projection as we did above. However, the equations still hold. One of the nice things about linear algebra is that we can visually see what happens when the vectors are in \(\mathbb{R}^2\) or \(\mathbb{R}^3\), but higher dimensions are fine, too. The projection equations are used in least squares regression, where we want as many rows of data as possible to accurately fit an equation to the data.
