6.11.2. Exact Solution or Approximation?¶
We know that the solution to an over-determined system is exact when
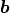 is in the column space of
is in the column space of 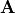 , but is an
approximation when it is not. The quickest way to determine if the
solution is exact or an approximation is to test if
, but is an
approximation when it is not. The quickest way to determine if the
solution is exact or an approximation is to test if 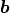 is
independent or a linear combination of the columns of
is
independent or a linear combination of the columns of 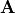 .
.
Vector
is in the column space of
when the ranks of
and the augmented matrix
are the same, which means that
is a linear combination of the columns of
.
MATLAB can help us see this. First, let us consider the case where
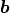 is in the column space of
is in the column space of 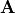 and an exact
solution exists. Notice that
and an exact
solution exists. Notice that rank(A) is equal to rank([A b]).
>> f = @(t) 5 - 2.*t;
>> t = 1:5;
>> A = ones(5,2);
>> A(:,2) = t';
>> A
A =
1 1
1 2
1 3
1 4
1 5
>> b = f(t)';
>> rank(A)
ans =
2
>> rank([A b])
ans =
2
>> x = A\b
x =
5.0000
-2.0000
Now, let’s add some random noise to the 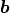 vector so that it
is not in the column space of
vector so that it
is not in the column space of 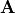 and the solution is an
approximation. Notice that
and the solution is an
approximation. Notice that rank(A) is less than rank([A b]).
>> b = b+randn(1,5)';
>> rank(A)
ans =
2
>> rank([A b])
ans =
3
>> x = A\b
x =
5.6816
-2.1410
