6.11.3. A Statics Problem Solved With Projections¶
Another application of projections comes from geometry. Projections relate two vectors as sides of a right triangle. Thus, projections can be used to solve problems that could also be solved using trigonometry. With projections, it is unnecessary to compute angles between the vectors or use the trigonometry functions.
Consider an example of a wagon sitting on an incline as shown in figure Fig. 6.28. The handle of the wagon is held at an angle. We want to calculate the force on the handle required to keep the wagon from rolling down the incline. We won’t worry about the inefficiency of the wheels. The force from the handle needs only to counter the force from gravity. The script to find the required force on the wagon handle is listed below.

Fig. 6.28 A wagon on an incline¶
NOTE: All vectors and forces are calculated as upward and to the right. The force from gravity, \(f_g\), will be negative. Then, the important statics equation is that the sum of forces equals zero. In the calculations, projection matrices are denoted as \(\bf{P}\). For clarity in the code, vector variables begin with capital letters, while scalar variables are lowercase.
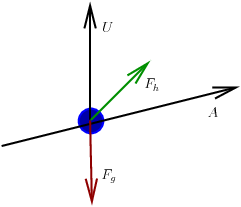
Fig. 6.29 Free-body diagram of forces on the wagon¶
The force toward the left (down the incline) is the projection of the gravity force onto the incline, \(\bm{A}\).
The sum of the forces to the left and right is zero.
The force to the right is a projection of the handle force vector onto the incline. The handle force vector is the product of the scalar force vector and the unit vector in the direction of the handle, \(\bm{F}_h = f_h\,\bm{H}\). We need to calculate the inverse of the projection, so we separate the scalar from the unit vector to include the vector direction in the calculation.
%% File: wagon.m
% Statics problem of a wagon on an incline solved with vector
% projections
P = @(a) a*a'/(a'*a); % Projection matrix equation
V = [0 1]'; % Vertical vector
A = [8 3]'; % vector of the incline slope
H = [1 1]'; % vector of handle direction
H = H/norm(H); % unit vector of handle direction
% Fh = fh*H
fg = 23 * -9.81; % Gravity force down (F = m*a)
% 23 kg is about 50 pounds
Fg = fg * V; % Gravity force vector
Pa = P(A); % Projection matrix to incline A
Fl = Pa * Fg; % force down hill to left
Fr = -Fl; % force to right, Fr + Fl = 0
fh = (Pa * H) \ Fr; % Fr = Pa*Fh = Pa*H*fh
fprintf('Force on handle = %.3f newtons or %.3f kg\n', ...
fh, fh/9.81);
Note
Now complete the Projection of Static Force Vectors homework assignment.
