3.2. Basic Line Plots

MathWorks has prepared a lot of documentation and videos on plotting, so some links to their documentation follows.

Here is an introductory video demonstrating line plotting.

Documentation on 2-D Graph and customize lines.

Documentation on 2-D and 3-D plots.

Documentation on the linespec portion of a plot command.

MathWork’s MATLAB Fundamentals course [FUNDAMENTALS] has a good introduction to creating plots.

3.2.1. Basic Plotting Notes

The Plot Tool is easy to use; however, using commands and functions allows for easier reproduction of plots and more automation. Use the plot(x, y) function to plot vector y against vector x. If only a single vector is passed to plot, then the index values of the vector are used for the \(x\) axis.

Use an additional argument to the plot function to change the color of the data curve. The following command makes a magenta plot of the \((x, y)\) values in row vectors x and y.

>> plot(x, y, 'm')

The color codes are:

’k’ black ’b’ blue ’g’ green

’r’ red ’c’ cyan ’m’ magenta

’w’ white ’y’ yellow

Use line style codes if you want something other than a solid line. The following command will plot y versus x with a dotted line.

>> plot(x, y, ':')

The line style codes are:

’-’ solid ’:’ dotted

’–’ dashed ’-.’ dash-dot

You can combine these codes. Generally, the order does not matter, so both of the following commands make a plot using a red dotted line.

>> plot(x, y, 'r:')
>> plot(x, y, ':r')

In addition to color and line style, you can specify a marker style. The following command will plot y versus x using asterisks.

>> plot(x, y, '*')

Some of the marker style codes are:

’.’ points ’o’ circles ’*’ asterisks

’x’ crosses ’+’ plus sign ’s’ square

’d’ diamond ’^’ upward-pointing triangle ’v’ downward-point triangle

If the only plot specification is a marker, the default line style is none. Add a line style, such as a dash (-), to the marker style to also plot a line.

The grid command adds or removes a grid to your plot:

>> grid on

>> grid off

3.2.2. Annotating Plots

Labels are added to plots using plot annotation functions such as xlabel, ylabel, and title. The input to these functions must be text. Traditionally, the textual data was entered as a character array made with characters and digits inside a pair of ’apostrophes’ (single quotation marks). MATLAB now allows text labels that are the newer string arrays made with characters and digits inside a pair of "quotation marks". The text may be a simple textual constant or be held in a variable. See Text Strings in MATLAB for more information on textual data.

>> xlabel('Text Label for X Axis') % a text constant

>> ylabel(yAxisName)               % a text variable

If you need more than one line in an axis label or title, use a cell array created with a pair of curly brackets {}.

>> title(\{'first line', 'second line'\})

LaTeX markup formatting may be used in the annotations. Thus, x^2 will become \(x^2\) and x_2 becomes \(x_2\). Latex markup is a default standard for mathematical equations. You can search the Internet for good documentation on formatting Latex math equations. Other symbols, such as Greek letters, can also be added, such as \(\Delta\), \(\gamma\), and \(\pi\). See MathWorks documentation on Greek Letters and Special Characters [Greek]. Try the following code to see what happens.

>> xlabel('/sigma \textbackslash{}approx e^\{\textbackslash{}pi/2\}')

If you need to use a symbol such as an underscore (_) or a backslash (\), then preface it with the escape character \. Thus, to display \, you must type \\.

The MATLAB text function adds a text annotation to a specified position on the plot. See the MATLAB documentation for text.

>> text(3, 5, 'Best result')

3.2.3. Starting a New Plot

You may notice your plot being replaced when you enter a new plot command after making a previous plot. Use the figure command to keep the previous plot and start over in a new window.

3.2.4. Multiple Plots in the Same Figure

Several small plots may be put in a figure. The subplot(m, n, p) function accomplishes this by making a grid of \(m{\times}n\) plots. The variable p is the plot number from 1 to \(m{\times}n\). The plot for the following code is shown in figure Fig. 3.3.

>> x = linspace(-5, 5);
>> subplot(2, 2, 1), plot(x, x), title('y = x')
>> subplot(2, 2, 2), plot(x, x.^2), title('y = x^2')
>> subplot(2, 2, 3), plot(x, x.^3), title('y = x^3')
>> subplot(2, 2, 4), plot(x, x.^4), title('y = x^4')

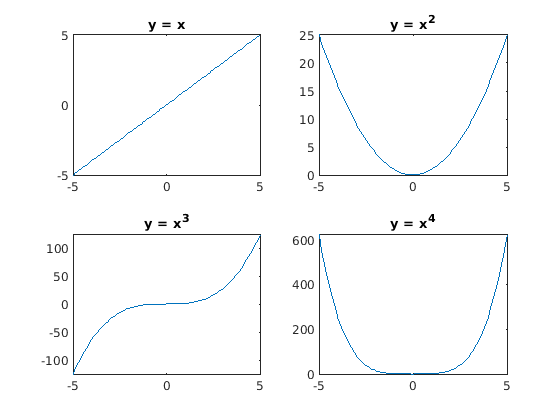
Fig. 3.3 Plots created using subplots

Enhanced subplots with the tiledlayout function were introduced in MATLAB release R2019b. As with subplot, creating a fixed layout grid of tiled plots is simple.

>> tiledlayout(2, 2);

The nexttile command is used to advance to the next plot. Several new features were added beyond the capabilities of subplots.

• Figures may now have a global title, xlabel, and ylabel for the set of plots.

• The size and spacing between tiles are adjustable. The following commands reduce the spacing between tiles and the padding between the figure’s edges and the tiles’ grid. The net effect is to increase the size of the individual plots.

  t = tiledlayout(3, 3);
  t.TileSpacing = 'compact';
  t.Padding = 'compact';
  

• Specifying the size and location of tiles creates a custom layout by passing a tile number and an optional range of tiles to the nexttile command. The example in figure Fig. 3.4 shows a \(3{\times}3\) grid of tiles. Three plots are added across the first row. Starting at tile 4, the second row is filled with the next plot, spanning a \(1{\times}3\) set of tiles. The third row has a single tile plot and a \(1{\times}2\) tile plot.

  >> x = linspace(-2,2);
  >> tiledlayout(3,3)
  >> nexttile, plot(x,x)
  >> nexttile, plot(x,x)
  >> nexttile, plot(x,x)
  >> nexttile(4, [1 3])
  >> plot(x,x)
  >> nexttile(7), plot(x,x)
  >> nexttile(8, [1 2])
  >> plot(x,x)
  

  

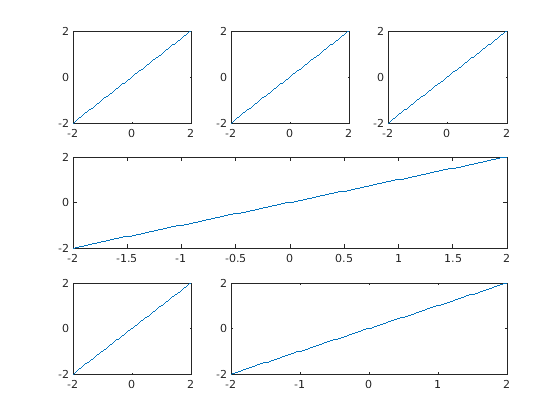
  Fig. 3.4 Tiled plots with a custom layout

• The ’flow’ option to tiledlayout adjusts the layout of the plots with each nexttile command. The first plot fills the whole figure. After the second plot, two stacked plots are shown. As each tile is added, the layout of tiles is adjusted to accommodate the new tile, which can show successive changes to data. Run the code from the sawTooth.m file to see this. Successive plots show the Fourier series of a sawtooth wave as each new sine wave is added. The user presses the Enter key when they are ready to see the next plot. The final tiled figure with six plots is shown in figure Fig. 3.5.

Sawtooth wave Fourier Series

The sawtooth wave is a periodic waveform used in various electrical circuits, including music synthesizers. The Fourier series for a sawtooth wave with amplitude of 1 and period of \(L\) is given by:

\[f(t) = \frac{1}{2} - \frac{1}{\pi} \sum_{n = 1}^{\infty} \frac{1}{n} \sin(2\,\pi\,n\,t/L)\]

% File: sawTooth.m
% Plots of the Fourier series of a sawtooth function
% displayed using a tiledlayout. Each time through
% the loop, a new plot is added.

clear; close all
L = 5;
N = 200;
t = linspace(0, 2*L, N);
s = zeros(1, N);
figure
plt = tiledlayout('flow');
title(plt, 'Sawtooth Fourier Series')
for n = 1:6
    nexttile
    s = s + sin(2*pi*n*t/L)/n;
    f = 0.5 - s/pi;
    plot(t, f, 'k', 'LineWidth', 2)
    title(['n = ', num2str(n)])
    if n < 6
        disp('Press enter for next plot')
        pause
    end
end

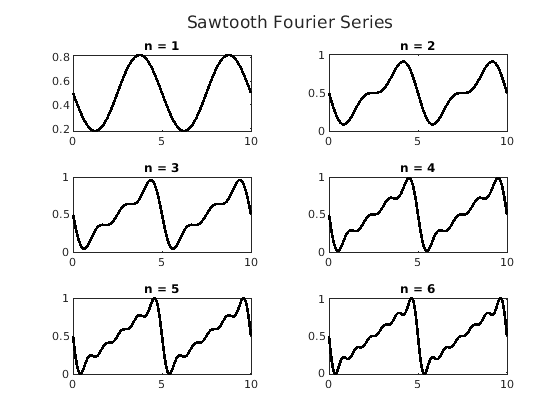
Fig. 3.5 Final sawtooth plots with six tiles

3.2.5. Multiple Plots on the Same Axis

Visualizations are often more informative when multiple data sets are plotted on the same axes. To add new plots onto an existing axis without replacing the previous plot, use the hold on command. When you are done adding plots, issue the hold off command. Then, unless a new figure is started, the next plotting command issued will replace what is currently in the figure.

Another way to plot multiple data sets onto a single figure is to put the \(y\) values in a matrix. Each column of the matrix will be a different plot. The following simple examples illustrate both methods. See figure Fig. 3.6 for the plot.

>> % Plot curves from the columns of Y
>> x = linspace(0,10); Y = zeros(100,3);
>> Y(:,1) = x; Y(:,2) = 2*x; Y(:,3) = 3*x;
>> plot(x, Y)

>> % Multiple curve plots on same axes
>> y1 = x; y2 = 2*x; y3 = 3*x;
>> hold on
>> plot(x, y1, 'k'), plot(x, y2, 'k:'), plot(x, y3, 'k-.')
>> hold off
>> xlabel('x'), ylabel('y')
>> legend('y = x', 'y = 2x', 'y = 3 x', 'Location', 'northwest')
>> title('Multi-line Plot')

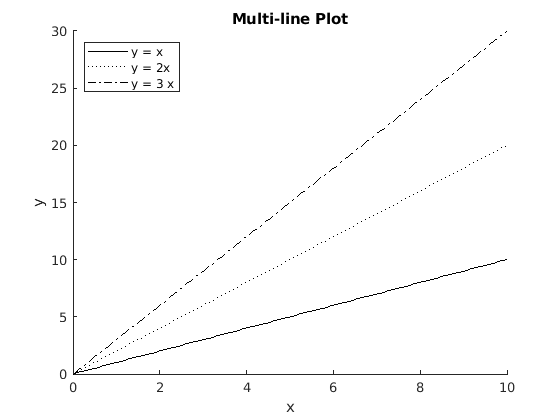
Fig. 3.6 Figure with multiple plots

3.2.6. Adding a Plot Legend

A legend helps identify what data each plot in the graph corresponds to. The order of legend labels matters—the inputs to legend should be in the same order in which the plots were drawn.

legend('first label', 'second label')

The legend function also accepts two optional arguments: the keyword ’Location’ and a text description of the location that is given by a compass direction, such as ’north’ (top center) or ’southwest’ (lower left). The default location for the legend is ’northeast’ (top right).

legend('Trucks', 'Cars', 'Location', 'west')

3.2.7. 2-D Plot Types

MATLAB supports several types of two-dimensional plots. Six types of plots other than basic line plots are described below. Example code to make these plots is also listed below, and figure Fig. 3.7 shows what the plots look like.

Scatter Plot

scatter(x, y): Scatter plot with variable marker size and color. Example shown in figure Fig. 3.7 (a).

Bar graph

bar(x, y): Bar graph (vertical and horizontal). Example shown in figure Fig. 3.7 (b).

Stem plot

stem(x, y): A discrete sequence plot—each point is plotted with a marker and a vertical line to the \(x\) axis. Example shown in figure Fig. 3.7 (c).

Stair step plot

stairs(x, y): The lines on the plot are either horizontal or vertical, resembling the run and rise of stairs. Example shown in figure Fig. 3.7 (d).

Pie chart

pie([0.4 0.3 0.2 0.1], labels): The values of the data are passed as a vector that often sums to 1; otherwise, MATLAB will calculate the percentages. The labels of the pie slices should be in a cell array. Example shown in figure Fig. 3.7 (e).

Filled area plot

area(x,[y1; y2]’): Plot multiple data sets with the area between the \(x\) axis and each data curve shaded a different color. Each data set is in a matrix column passed as the \(y\) data. Example shown in figure Fig. 3.7 (f). Note that if the \(y\) data is in row vectors, then a transpose may be needed to put the data in the columns of the \(Y\) matrix.

% File: Plots2D.m
% Some 2-D plotting examples

x = linspace(0, 2, 10);
y = 5 + x.^2;
y2 = 5 + x;
plts = tiledlayout(3, 3);
plts.TileSpacing = 'compact';
plts.Padding = 'compact';
title(plts, '2-D Plots');
nexttile, scatter(x, y, 'ko'), title('(a) Scatter Plot');
nexttile, bar(x, y, 'k'), title('(b) Bar Chart');
nexttile, stem(x, y, 'k'), title('(c) Stem Plot');
nexttile, stairs(x, y, 'k'), title('(d) Stairs Plot');
labels = \{'excellent', 'good', 'fair', 'poor'\};
nexttile(5, [2 2]), pie([0.4 0.3 0.2 0.1], labels)
title('(e) Pie Chart')
newcolors = [0.7 0.7 0.7; 0.2 0.2 0.2]; % make grayscale
nexttile(7), area(x, [y2; y]'), title('(f) Area Plot');
colororder(newcolors)

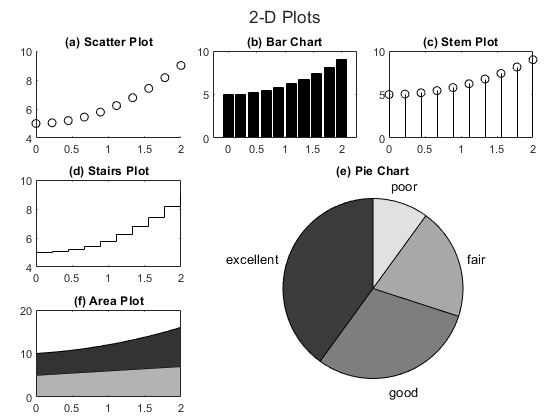
Fig. 3.7 Common types of 2-D plots other than line plots

3.2.8. Axis Control

The axis command returns a 4-element row vector containing the \(x\) and \(y\) axis limits.

>> v = axis
v =
    10 20 1 5

Use the xlim and ylim functions to set the \(x\) and \(y\) axis limits. Both functions take a vector of two elements as input. For example, the following command sets the \(y\) axis range between 2 and 4.

>> ylim([2 4])

Use the axis tight command to change the limits based on the range of the data.

We would like the \(x\), \(y\), and \(z\) axes to have the same scale for plots depicting geometry. There are two ways to accomplish this. The axis command has an equal option that sets the scale of each axis to be the same. We can also set the aspect ratio to be the same for each axis with the daspect function, which takes a vector with three values, even for 2-D plots.

>> axis equal        % Set the axes scales to be the same
>> %                 % or
>> daspect([1 1 1])  % Another way to accomplish the same

3.2.9. Tick Marks and Labels

MATLAB usually does a good job setting the tick marks on a plot. The tick labels are, by default, the numeric values of the tick marks. We sometimes want to change the labels and locations of the tick marks because specific points on the axis have significance. A good example of this is when plotting equations that use trigonometric functions.

The xticks and yticks functions take vectors of numeric locations for the tick marks. The xticklabels and yticklabels functions take cell arrays of textual data. See Text Strings in MATLAB for more information on cell arrays. The following code illustrates custom tick marks and labels on the \(x\) axis. Notice also that the title uses the texlabel function to format strings with LaTeX to match an equation. The plot is shown in figure Fig. 3.8.

x = linspace(pi/4, 5*pi/4);
figure, plot(x, 4 - 4*sin(2*x - pi/2))
txt = texlabel('f(x) = 4 - 4*sin(2*x - pi/2)');
title(txt), ylabel('f(x)'), xlabel('x')
xticks(linspace(pi/4, 5*pi/4, 5))
xticklabels(\{'/pi/4', '\textbackslash{}pi/2', '3\textbackslash{}pi/4','\textbackslash{}pi', '5\textbackslash{}pi/4'\});
axis tight

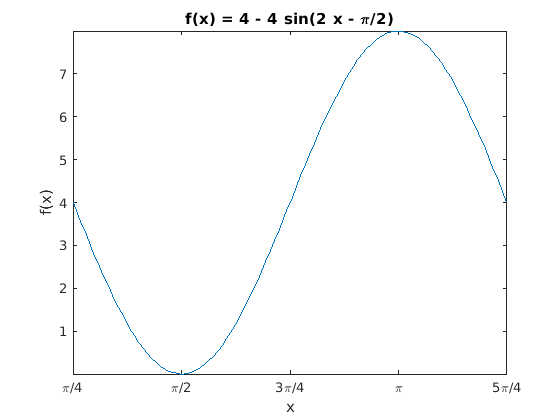
Fig. 3.8 Sine wave with TeX formated \(x\)–axis tick marks and title.