3.3. 3-D Plots

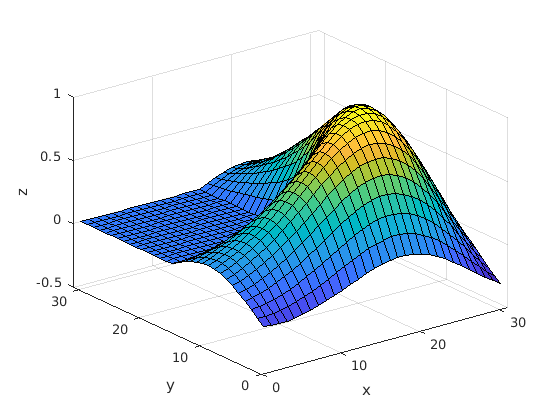
MATLAB has several functions for plotting data in three dimensions. Try this code. The membrane data is built into MATLAB.

>> m = membrane;
>> surf(m)
>> xlabel('x')
>> ylabel('y')
>> zlabel('z')
../_images/membrane.png

Do you recognize the shape of the data?

Given only a matrix as input, the 3-D surface plotting functions will show the matrix values as the z–axis values and use the matrix indices for the x– and y–axis.

The meshgrid function is used to create matrices of the x– and y–axis values that cover the range of data. Using data created from meshgrid, the z–axis values are simple to create from an equation.

>> x = -3:3;
>> y = -3:3;
>> [X, Y] = meshgrid(x,y);
>> X
X =
    -3    -2    -1     0     1     2     3
    -3    -2    -1     0     1     2     3
    -3    -2    -1     0     1     2     3
    -3    -2    -1     0     1     2     3
    -3    -2    -1     0     1     2     3
    -3    -2    -1     0     1     2     3
    -3    -2    -1     0     1     2     3
>> Y
Y =
    -3    -3    -3    -3    -3    -3    -3
    -2    -2    -2    -2    -2    -2    -2
    -1    -1    -1    -1    -1    -1    -1
     0     0     0     0     0     0     0
     1     1     1     1     1     1     1
     2     2     2     2     2     2     2
     3     3     3     3     3     3     3
>> Z = X.^2 + Y.^2
Z =
    18    13    10     9    10    13    18
    13     8     5     4     5     8    13
    10     5     2     1     2     5    10
     9     4     1     0     1     4     9
    10     5     2     1     2     5    10
    13     8     5     4     5     8    13
    18    13    10     9    10    13    18

3.3.1. 3-D Plot Functions

Here are descriptions of some of the 3-D plots available in MATLAB. Examples of the plots are shown in Fig. 3.10 and Fig. 3.11. The data for the plots is from the following code. Except for the plot3 function, the X, Y, and Z data is a two dimension grid of values, such as produced by the meshgrid function.

x = -8:0.25:8;
y = -8:0.25:8;
y1 = 8:-0.25:-8;
t = x.^2 + y1.^2;
z = (y1-x).*exp(-0.12*t); % for plot3
[X, Y] = meshgrid(x,y);
T = X.^2 + Y.^2;
Z = (Y-X).*exp(-0.12*T); % for surface plots
../_images/plots3D1.png

Fig. 3.10 Three Dimensional Plots: (a) surf, (b) surfc, (c) mesh, (d) plot3.

surf

surf(X, Y, Z): A three-dimensional surface plot. Probably the most often used 3-D plot function. Example shown in Fig. 3.10 (a). https://www.mathworks.com/help/matlab/ref/surf.html

surfc

surfc(X, Y, Z): A contour plot under a surface plot. Example shown in Fig. 3.10 (b). https://www.mathworks.com/help/matlab/ref/surfc.html

mesh

mesh(X, Y, Z): A wireframe mesh with color determined by Z, so color is proportional to surface height. Example shown in Fig. 3.10 (c). https://www.mathworks.com/help/matlab/ref/mesh.html

plot3

plot3(x, y, z): A line plot, like the plot function, but in 3 dimensions. Example shown in Fig. 3.10 (d). https://www.mathworks.com/help/matlab/ref/plot3.html

../_images/plots3D2.png

Fig. 3.11 Three Dimensional Plots: (a) contour, (b) contour3, (c) meshz, (d) waterfall.

contour

contour(X, Y, Z): A contour plot displays isolines to indicate lines of equal z–axis values, like found on a topographic map. Example shown in Fig. 3.11 (a). https://www.mathworks.com/help/matlab/ref/contour.html

contour3

contour3(X, Y, Z): A 3-D contour plot. Not all data shows well with contour type plots. Example shown in Fig. 3.11 (b). https://www.mathworks.com/help/matlab/ref/contour3.html

meshz

meshz(X, Y, Z): Like a mesh plot, with a curtain around the wireframe mesh. Example shown in Fig. 3.11 (c). https://www.mathworks.com/help/matlab/ref/meshz.html

waterfall

waterfall(X, Y, Z): A mesh similar to the meshz function, but it does not generate lines from the columns of the matrices. Example shown in Fig. 3.11 (d). https://www.mathworks.com/help/matlab/ref/waterfall.html

surfl

surfl(X, Y, Z): A shaded surface based on a combination of ambient, diffuse, and specular lighting models. Color is required for this plot to look right and the effect will vary depending on the data. An example plot is not shown. https://www.mathworks.com/help/matlab/ref/surfl.html

Tip

Sometimes a 3-D plot will at first look like as a 2-D plot. Before concluding that you made a mistake, use the rotate tool to move the plot around. Sometimes 3-D plots first show a view of the plot that make it look a 2-D plot when it is actually a 3-D plot.

3.3.2. Axis Orientation

If the axes are not labeled, it may be hard to remember which is the x–axis and the y–axis. Use the right hand rule to help with this. Point your right index finger in the direction of the x–axis. Hold your middle finger at 90 degrees, which will be in the direction of the y–axis. Your thumb will be in the direction of the z–axis. See Fig. 3.12 for the correct 3-D coordinate frame layout.

A physical model is also helpful to visualize the 3-D coordinate frame axes. One can be printed on a 3-D printer. For a paper model, Peter Corke’s web-site has a PDF file that can be printed, cut, folded, and glued. The PDF file is available at http://www.petercorke.com/axes.pdf

../_images/axis_right_hand_rule.png

Fig. 3.12 3-D coordinate frame and the right hand rule.

../_images/index_rhr.jpg

Fig. 3.13 Right hand rule