14.7. The Flight of a Home Run Baseball

It was the bottom of the ninth inning of game 1 of the 2015 World Series. The New York Mets led the Kansas City Royals 4 to 3 with one out in the bottom of the ninth inning and then this happened. Watch the video and make note of two things – how long was the ball in the air (measure with a stop-watch), and estimate how far the ball went before hitting the ground. I used t_f = 5.9 seconds. The marker on the wall gives us a starting point to estimate how far the ball went. I used x_f = 438 feet.

You are to write a MATLAB script that will plot the vertical and horizontal path of the ball. Fig. 14.1 shows an example plot. The script should also display the maximum height, initial velocity, and initial projection angle of the ball. The steps listed below will guide you.

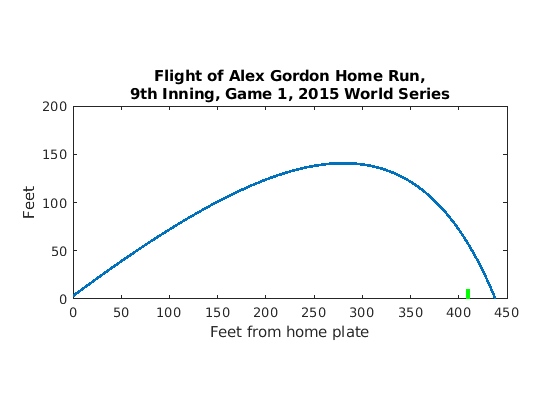
../_images/HomeRun.png

Fig. 14.1 Example Plot

The horizontal and vertical paths of the ball may be calculated independently.

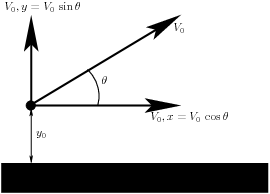
../_images/baseball.png

Fig. 14.2 The ball begins at an initial height. It has an initial velocity at an initial projection angle. The initial velocity may be split into horizontal and vertical components.

  1. First make variables for constant values – gravity: g = -32 feet/sec^2, final time of flight: t_f in seconds, Initial height: y_0 = 3 feet, and the final horizontal displacement: x_f in feet. Also use linspace to make a 100 element vector, t for time from 0 to t_f.

  2. The vertical path of the ball may be treated the same as for throwing a ball straight up. The only force on the ball worth noting is gravity. The height of the ball is given by

    y = y_0 + V_{0,y}\,t + 1/2\,g\,t^2

    Using the t_f value measured with the stop watch, calculate V_{0,y}, which occurs when y = 0. The y path of the ball may be calculated now.

  3. Next use the final horizontal displacement, x_f, to calculate the initial horizontal velocity. Air resistance will slightly slow the horizontal displacement [ADAIR90] according to the differential equation,

    \frac{dv_x(t)}{dt} = - 0.2\,v_x(t).

    The solution to the differential equation is

    v_x(t) = V_{0,x}\,e^{-0.2\,t}.

    Then, the displacement comes from the definite integral of the velocity.

    x(t) = V_{0,x}\int_0^t e^{-0.2 \tau} d\tau = 5\,V_{0,x}(1 - e^{-0.2\,t}).

    The constant value of 0.2 is an estimated, typical value. The real value is dependent on other factors such as the wind speed and direction that we don’t know.

    From simple trigonometry, V_0, and \theta can be expressed in terms of V_{0,y} and V_{0,x}. Hint: Use the atan2d function to find \theta.

  4. Plot the path with a 'LineWidth' of 2.

    Show the home run wall by plotting a green line with 'LineWidth' of 3. Make the wall 10 feet tall at 410 feet from home plate.

    Remember to annotate the plot and to report the maximum height, initial velocity, and initial projection angle of the ball.

MATLAB Grader Assignment Page

In addition, save the plot to a png file and submit it to the Canvas assignment page.