3.2. Transformations in 3-DΒΆ
If you have not read the introductory comments in Transformations in 2-D, do so now.
The pose of a robot, or robot part in three dimensions consists of six
elements. Three values define the position and three rotation angles define
the rotation about the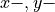 
, and 
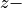axis. Note that the
order of the rotations matters to the orientation.
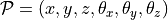
Rotation matrices in 3-D are 3-by-3 matrices, and homogeneous transformations are defined by 4-by-4 matrices.
The orientation direction of the three axes requires consideration, especially after some rotations. Use the right hand rule to help with this. Point your right index finger in the direction of the x-axis. Hold your middle finger at 90 degrees, which will be in the direction of the y-axis. Your thumb will be in the direction of the z-axis.
A 3-D coordinate frame axes model also helps to visualize rotations. This model can be printed, cut, folded, and glued.
The other form of the right hand rule shows the direction of a positive rotation angle. Point your right thumb in the direction of the axis to be rotated around and curl your fingers. Your finger tips will point in the direction of a positive rotation angle.
