3.1. Transformations in 2-D

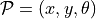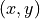We previously defined the robot’s pose (see The Pose of a Robot). For robots that move in two dimensions, such as a mobile robot or arm type robots that move in a plane, the robot’s pose is a three element vector: . An alternative expression of the pose is to define it as a coordinate frame. The coordinate frame consists of two perpendicular (orthogonal) axis and an point location of the origin of the coordinate frame. The coordinate frame pose is usually expressed by a matrix. This allows us to express the coordinate frame of connected parts and joints of the robot with respect to other coordinate frames. Then by matrix multiplication and linear algebra, we can easily determine a coordinate frame with respect to the world frame, or any other frame of interest.

We will begin the discussion of coordinate frames, rotation, translation, and pose in two dimensions. The concepts described in two dimensions can then be extended to three dimensions.

• 3.1.1. Rotation of a Point
• 3.1.2. Homogeneous Matrix
  • 3.1.2.1. Applying Transformations to a Point
  • 3.1.2.2. Homogeneous Transformation
• 3.1.3. Coordinate Transformations in 2-D