17.3. Continuous 1D Fourier Transform

The Fourier Series previously considered is intended for use with periodic signals. More general signals may exhibit some locally periodic components, but are not, in general, periodic. The Fourier transform and the inverse Fourier transform allow for the conversion of any signal to the frequency domain and back again to either the time or spatial domain.

We consider one dimensional signals only as steps towards the 2-D Fourier transform of images. One dimensional continuous and discrete signals provide simpler cases for learning some of the important properties of frequency domain data.

Fourier Transform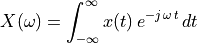

X(\omega) = \int_{-\infty}^{\infty} x(t) \, e^{-j\,\omega\,t} \, dt

Where 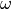\omega is a continuous frequency in radians/sec.

Inverse Fourier Transform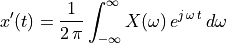

x'(t) = \frac{1}{2\,\pi} \int_{-\infty}^{\infty} X(\omega) \, e^{j\,\omega\,t} \, d\omega

Properties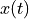
  • x(t) is continuous and may be complex.
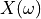  • X(\omega) is complex and continuous.
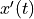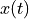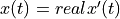  • x'(t) is complex, but if x(t) was real, then x(t) = real{ x'(t) }.
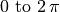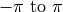  • Although it is a bit hard to think about negative frequencies, they are a mathematical necessity. This is because of the cyclical nature of the complex exponential. The values of the complex exponential over the range 0 \mbox{ to } 2\,\pi are the same as for the equivalent range -\pi \mbox{ to } \pi.

17.3.1. Common Fourier Transform Pairs

Below are some common frequency and time domain pairs. These results will be useful to us for explaining other properties later.

../_images/common_FT_pairs.png