11.4. Numerical Integration

Numerical integration is an important numerical method because analytic solutions are often unavailable. Surprisingly, the seemingly simple equation \(y = e^{-x^2}\) can not be integrated analytically.

A definite integral is an area calculation. illustrated that the value of a definite integral is the area bounded by the function, the \(x\) axis, and the lower and upper bounds of the integral.

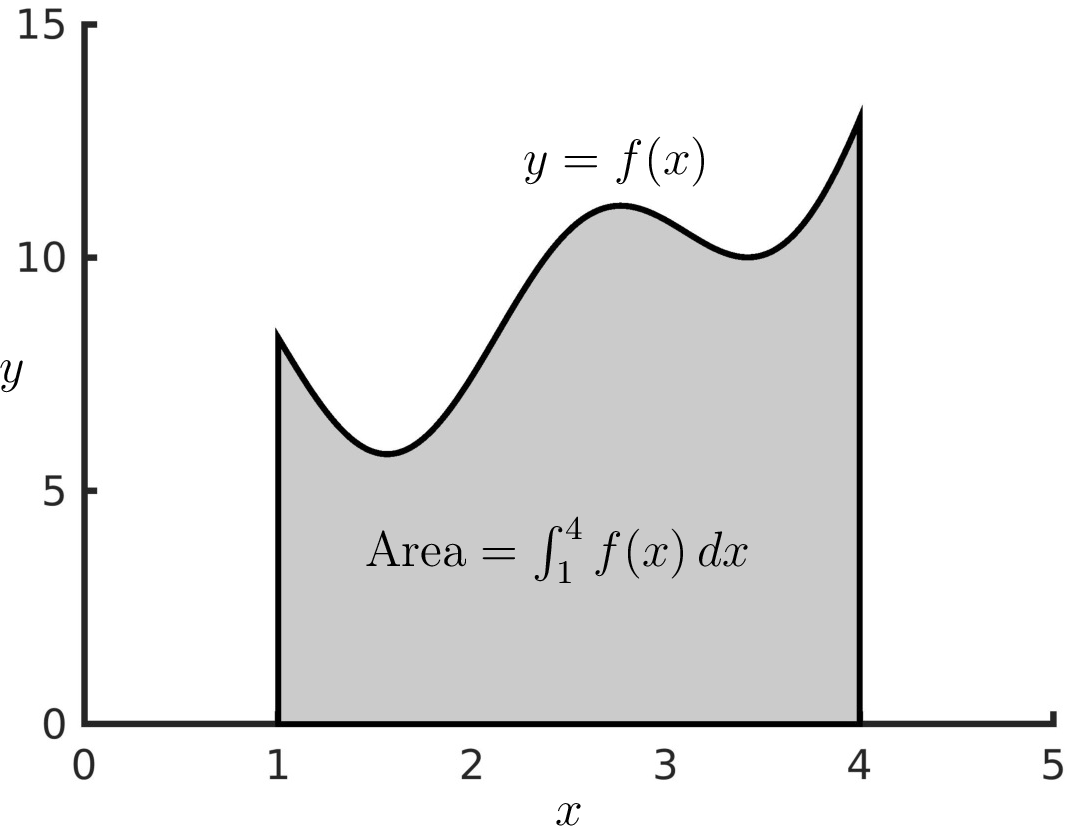
Fig. 11.12 A definite integral is an area calculation.

Numerical techniques estimate the area by summing the areas of a sequence of thin slices (subintervals). Three such techniques are commonly used to estimate the area of each subinterval. The Riemann Integral uses rectangular regions to estimate the area of each small subinterval. The Trapezoid Rule improves the results by modeling the area of each subinterval as a trapezoid. Simpson’s Rule provides a more accurate estimate by modeling the curve over a pair of subintervals as a quadratic polynomial.

11.4.1. MATLAB’s Integral Function

MATLAB has a function for computing definite integrals called integral, which replaces an older function called quad. The integral function uses a global adaptive quadrature algorithm where the integration region is divided into piecewise smooth regions before integrating each subinterval. The widths of the subintervals are adapted so that an equation accurately models each subinterval.

The integral function is called with arguments of a function handle and the interval of the integral (I = integral(f, a, b)). Be sure to use element-wise arithmetic operators when defining the function so that it can accept and return vectors. The integration interval is normally specified with a pair of real scalars, but negative and positive infinity (-Inf and Inf) may be used. See MATLAB’s documentation for information about complex functions, and the use of tolerances and waypoints.

Here are a few usage examples.

>> integral(@(x) sin(x), 0, pi)
ans =
    2.0000
>> integral(@(x) exp(-2*x), 0, Inf)
ans =
    0.5000
>> f = @(x) x.^2 - 5.*x + 8;
>> integral(f, 1, 4)
ans =
    7.5000

11.4.2. Fixed Width Subinterval Algorithms

Although one only needs MATLAB’s integral function to compute integrals numerically, learning the basics of the numeric integration algorithms is desirable. Knowledge of the algorithms helps one better understand and appreciate MATLAB’s functions. Still, writing an integration function in a programming language like C may be needed if MATLAB’s functions are unavailable. We will consider how to implement numeric integration algorithms using the trapezoid rule and Simpson’s rule. We do not discuss results from Riemann integrals because integrals from trapezoids are slightly more complex than Riemann integrals, but are more accurate.

11.4.2.1. Trapezoid Rule Integrals

The geometry of a trapezoid is illustrated in figure Fig. 11.13. When an integration region is divided into equal-width trapezoids separated by grid points \(\{x_0, x_1, \ldots, x_n \}\), then the width of each trapezoid is \(h = x_{i+1} - x_i\). The area of the trapezoid is the product of the width times the average height of the two sides.

\[\text{Area} = h\,\frac{f(x_i) + f(x_{i+1})}{2}\]

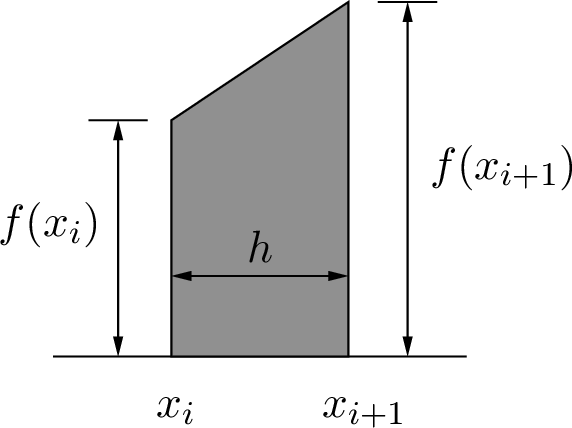
Fig. 11.13 The shape of a trapezoid and its size measurements

The definite integral of a function over a region from \(a\) to \(b\) is approximated by the sum of trapezoids found by splitting the region into \(n\) equal-width subintervals (also called panels), where \(n+1\) is the number of grid points that divide the interval into the subintervals. [1]

\[h = \frac{b - a}{n}\]

\[\int_{a}^{b} f(x)\,dx \approx \sum_{i=0}^{n - 1} h\,\frac{f(x_i) + f(x_{i+1})}{2}\]

In the summation, each term except the first and last appears twice because they are part of the calculation of two trapezoids.

\[\int_{a}^{b} f(x)\,dx \approx \frac{h}{2} \left(f(x_0) + 2\sum_{i=1}^{n - 1} f(x_i) + f(x_n) \right)\]

As shown in figure Fig. 11.14, the area of each trapezoid is sometimes more, less, or nearly the same as the true area of each subinterval. Using more subintervals, which reduces the size of \(h\), will improve the accuracy. With narrower subintervals, the spanned region of \(f(x)\) from \(x_i\) to \(x_{i+1}\) will more closely resemble a straight line. Of course, we need to be sensitive to the size of \(h\) to avoid excessive round-off errors when \(h\) is very small.

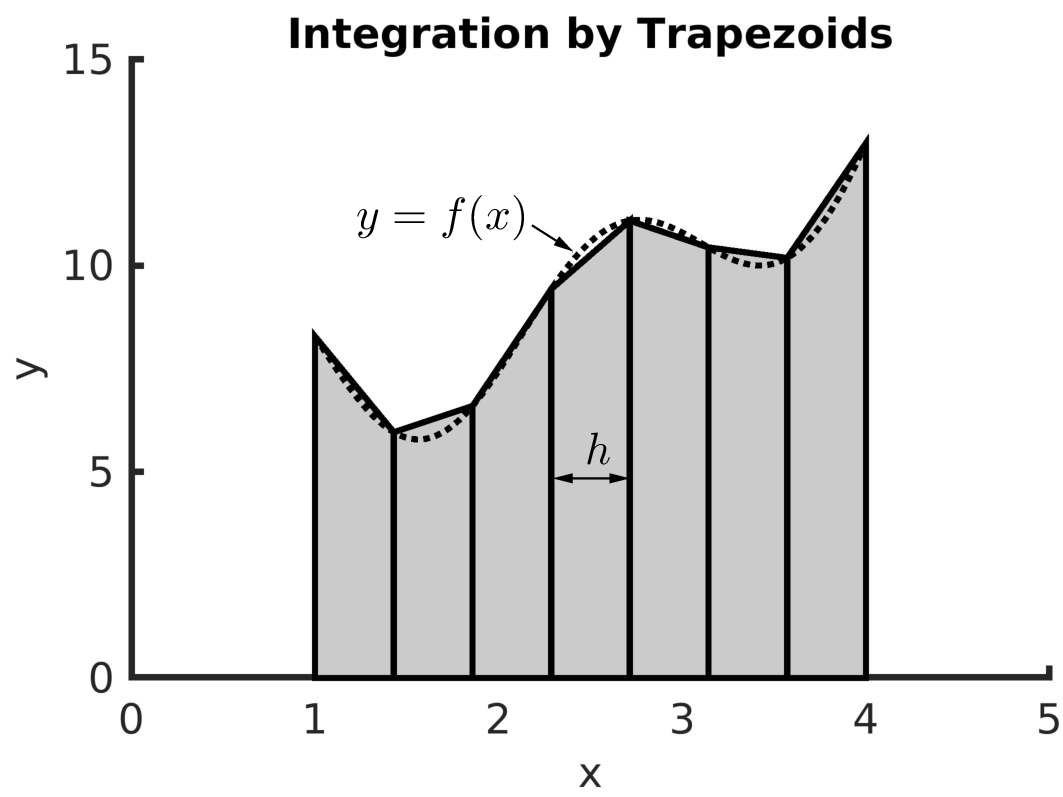
Fig. 11.14 The trapezoid rule models each subinterval as a trapezoid. The definite integral is the sum of the trapezoid areas.

The trapIntegral function implements the trapezoid rule to calculate an estimate of a definite integral.

function I = trapIntegral(f, a, b, n)
% TRAPINTEGRAL - Definite integral by trapezoid area summation.
%
% f - vector-aware function
% a - lower integration boundary
% b - upper integration boundary, a < b
% n - number of subinterval trapezoids

    if a >= b
        error('Variable b should be greater than a.')
    end
    h = (b - a)/n; x = linspace(a, b, n+1); y = f(x);
    I = (h/2)*(y(1) + 2*sum(y(2:end-1)) + y(end));

Tests using the trapezoid rule integration function show that it finds an answer that is somewhat close with a modest number of grid points, but struggles to find the true definite integral value, even as the number of grid points increases.

>> fun = @(x) x.^2;
>> trapIntegral(fun, 0, 4, 10)  %  correct = 21.3333
ans =
   21.4400
>> trapIntegral(fun, 0, 4, 50)
ans =
   21.3376
>> trapIntegral(fun, 0, 4, 100)
ans =
   21.3344

>> f = @(x) x.^2 - 3.*x + 2*sin(3*x).*exp(-0.01*x) + 10;
>> trapIntegral(f, 1, 4, 10)    %  correct = 27.30753
ans =
   27.4343
>> trapIntegral(f, 1, 4, 100)
ans =
   27.3088
>> trapIntegral(f, 1, 4, 500)
ans =
   27.3076

11.4.2.2. Simpson’s Rule Integrals

Rather than using a straight line to approximate the function over an integration subinterval, Simpson’s rule estimates the function as a parabola represented by a quadratic equation. Each integration region consists of two adjacent subintervals and three grid points. The three grid points are used to find the quadratic equation from which the area is computed. The development of the quadratic equation is covered in calculus textbooks and can also be found on several web pages. It is typically found from a Taylor series expansion of a quadratic equation or using Lagrange polynomial interpolation [SIAUW15].

Lagrange polynomial interpolation finds a polynomial that goes through data points. The Lagrange polynomial, \(P(x)\), has the property that \(P(x_i) = y_i\) for all given \((x_i, y_i)\) data points. We first find a Lagrange basis polynomial, \(P_i(x)\), for each given \(x_i\) value. The basis polynomials are products of factors such that \(P_i(x_i) = 1\) and \(P_i(x_j) = 0\) when \(i \neq j\). Then the Lagrange polynomial is a sum of products between the basis polynomials and the given \(y_i\) values. The properties of the basis polynomials ensure that the Lagrange polynomial passes through each point.

\[P_i(x) = \prod_{j=1, j\neq i}^n \frac{x - x_j}{x_i - x_j}\]

\[P(x) = \sum_{i=1}^n y_i\,P_i(x)\]

Lagrange Polynomial Example

Let us use Lagrange polynomial interpolation to find the quadratic equation that passes through the points \(\{(0, 2), (1, 5), \text{and } (2, 6)\}\).

\[\begin{split}\begin{array}{rl} P_1(x) &= \frac{(x - x_2)(x - x_3)}{(x_1 - x_2)(x_1 - x_3)} = \frac{(x - 1)(x - 2)}{(0 - 1)(0 - 2)} = \frac{1}{2}(x^2 - 3\,x + 2) \\ \hfill \\ P_2(x) &= \frac{(x - x_1)(x - x_3)}{(x_2 - x_1)(x_2 - x_3)} = \frac{(x - 0)(x - 2)}{(1 - 0)(1 - 2)} = -x^2 + 2\,x \\ \hfill \\ P_3(x) &= \frac{(x - x_1)(x - x_2)}{(x_3 - x_1)(x_3 - x_2)} = \frac{(x - 0)(x - 1)}{(2 - 0)(2 - 1)} = \frac{1}{2}(x^2 - x) \end{array}\end{split}\]

\[\begin{split}\begin{array}{rl} P(x) &= 2\,P_1(x) + 5\,P_2(x) + 6\,P_3(x) \\ &= (1 - 5 + 3)\,x^2 + (- 3 + 10 - 3)\,x + 2 \\ &= -x^2 + 4\,x + 2 \end{array}\end{split}\]

Figure Fig. 11.15 shows a plot of the quadratic equation.

>> P = @(x) -x.^2+4*x+2;
>> x = linspace(-1, 3);
>> y = P(x);
>> plot(x,y)
>> hold on
>> plot([0 1 2], [2 5 6], 'd', 'MarkerSize', 10)
>> hold off

Fig. 11.15 The Lagrange polynomial passes through the points \(\{(0, 2)\), \((1, 5)\), and \((2, 6)\}\).

Application of Simpson’s Rule

Figure Fig. 11.16 illustrates one region of integration. The quadratic equation \(P(x)\) passes through the three points \(\{(x_{i-1}, f(x_{i-1}))\), \((x_{i}, f(x_{i}))\), and \((x_{i+1}, f(x_{i+1}))\}\), which are the intersections between the three grid points and \(f(x)\). Using integration by substitution and some algebra, the definite integral of each integration region is given by

\[I_i = \int_{x_{i-1}}^{x_{i+1}} P(x)\,dx = \frac{h}{3}\left(f(x_{i-1}) + 4\,f(x_i) + f(x_{i+1})\right).\]

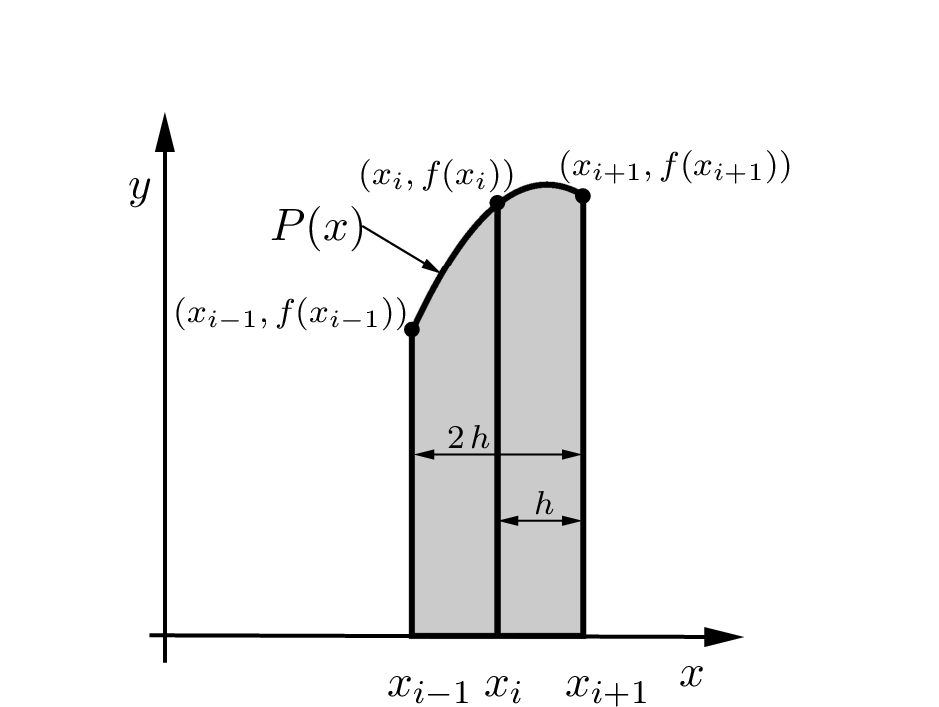
Fig. 11.16 Simpson’s rule subinterval integration

The sum of the subinterval integrals approximates the definite integral from \(a\) to \(b\). Since each integral spans two subintervals, the count of function values at even and odd grid points is different.

\[\int_a^b f(x)\,dx \approx \frac{h}{3}\left[f(x_0) + 4\left(\sum_{i = 1,\, i\, \text{odd}}^{n - 2} f(x_i)\right) + 2\left(\sum_{i = 2,\, i\, \text{even}}^{n - 1} f(x_i)\right) + f(x_n)\right]\]

Figure Fig. 11.17 shows that Simpson’s rule can find accurate definite integral results if the subintervals are small enough to model the function with quadratic equations accurately.

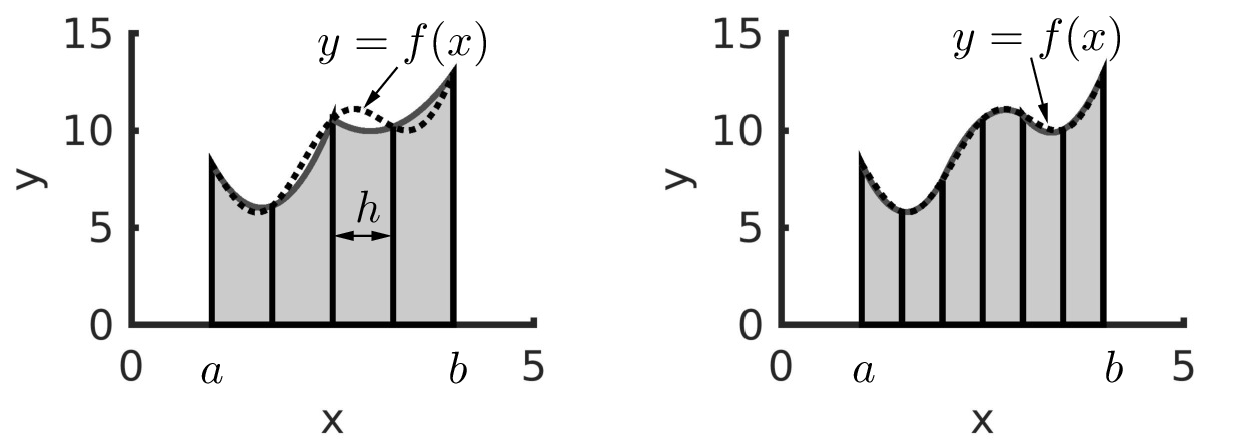
Fig. 11.17 Left: Simpson’s rule integration with five grid points, four subintervals, and two integration regions. Right: Simpson’s rule integration with 7 grid points, six subintervals, and three integration regions.

The number of subintervals must be even because Simpson’s rule computes integrals over two subintervals. So the number of grid points must be odd. To satisfy the indexing requirements of the sum functions in the MATLAB code, the minimum number of grid points is 5 (4-panel integration).

The simpsonIntegral function implements Simpson’s rule integration.

function I = simpsonIntegral(f, a, b, n)
% SIMPSONINTEGRAL - Definite integral by Simpson's rule.
%
% f - vector-aware function
% a - lower integration boundary
% b - upper integration boundary, a < b
% n - number of subintervals, must be an even number and >= 4

    if a >= b
        error('Variable b should be greater than a.')
    end
    if mod(n, 2) ~= 0 || n < 4
        error('Variable n, should be an even number, n >= 4.')
    end
    h = (b - a)/n; x = linspace(a, b, n+1); y = f(x);
    I = (h/3)*(y(1) + 4*sum(y(2:2:end-1)) ...
                    + 2*sum(y(3:2:end-2)) + y(end));
    %  MATLAB indexing starts at 1, so even and odd are reversed.

Tests show that Simpson’s rule integration is more accurate than trapezoid rule integration even with fewer subintervals.

>> fun = @(x) x.^2
>> simpsonIntegral(fun, 0, 4, 8)
ans =           %  correct = 21.3333
   21.3333

>> f = @(x) x.^2-3.*x+2*sin(3*x).*exp(-0.01*x)+10
>> simpsonIntegral(f, 1, 4, 8)
ans =           %  correct = 27.30753
   27.2950
>> simpsonIntegral(f, 1, 4, 18)
ans =
   27.3071
>> I = simpsonIntegral(f, 1, 4, 28)
I =
   27.3075
>> error = abs(I - integral(f, 1, 4))
error =         %  compare to MATLAB's integral
    7.1945e-05

11.4.3. Recursive Adaptive Integral

The recursive function adaptIntegral investigates the concept of an adaptive algorithm, like MATLAB’s integral function, that adjusts the width of each subinterval based on the accuracy of intermediate results. The basic concept of how the algorithm works is simple. If the function to be integrated fits the integration model (trapezoid or quadratic equation) over the integral region, then we have an accurate definite integral. However, the interval is divided into smaller subintervals if the integration model is a poor data fit.

For each interval, the algorithm splits the interval from \(a\) to \(b\) in half and calculates the area of three intervals. The interval from \(a\) to \(b\) is divided equally into subintervals from \(a\) to \(c\) and from \(c\) to \(b\). If the area from \(a\) to \(b\) is within a small tolerance of the sum of the areas of the subintervals, then the algorithm is satisfied with the area of the interval. Otherwise, the algorithm repeats by making recursive function calls for each subinterval. The algorithm splits each subinterval until the integration model accurately fits the function over the subinterval. The returned subinterval areas are added together to find the definite integral of the function from \(a\) to \(b\).

The adaptive function can use either the trapezoid rule or Simpson’s rule algorithm. The second argument should be either ’t’ or ’s’ to select the integration algorithm.

Tests that the adaptive interval algorithm accurately estimates definite integrals. Results from Simpson’s rule are more accurate than those from the trapezoid rule algorithm.

>> f = @(x) x.^2-3.*x+2*sin(3*x).*exp(-0.01*x)+10
>> I = integral(f, 1, 4);
>> I - adaptIntegral(f, 's', 1, 4)
    ans =         %  compare to MATLAB's integral
   2.4833e-12
>> I - adaptIntegral(f, 't', 1, 4)
ans =
  -8.4254e-10

>> s = @(x) sin(x);
>> adaptIntegral(s, 's', 0, pi)
ans =           %  correct = 2
   2.0000
>> 2 - ans
ans =
  -1.2683e-12
>> 2 - adaptIntegral(s, 't', 0, pi)
ans =
   1.5821-09

function I = adaptIntegral(f, intFun, a, b)
% ADAPTINTEGRAL - Adaptive interval definite integral.
%
% f - vector-aware function
% intFun - 't' for trapIntegral or 's' for simpsonIntegral
% a - lower integration boundary
% b - upper integration boundary, a < b
%
% This code demonstrates adaptive intervals.
% Use MATLAB's integral function, not this function.

    if a >= b
        error('Variable b should be greater than a.')
    end
    tol = 1e-12; c = (a + b)/2;
    % Three integrals
    if intFun == 't'
        Iab = trapIntegral(f, a, b, 2);
        Iac = trapIntegral(f, a, c, 2);
        Icb = trapIntegral(f, c, b, 2);
    elseif intFun == 's'
        Iab = simpsonIntegral(f, a, b, 4);
        Iac = simpsonIntegral(f, a, c, 4);
        Icb = simpsonIntegral(f, c, b, 4);
    else
        error("Specify 's' or 't' for intFun")
    end
    if abs(Iab - (Iac + Icb)) < tol
        I = Iac + Icb;
    else
        I = adaptIntegral(f, intFun, a, c) ...
            + adaptIntegral(f, intFun, c, b);
    end

[1]

Since MATLAB array indices start at 1, not 0, our code implementations set the grid points at \(\{x_1, x_2, \ldots, x_{n+1}\}\).