11.3. Numerical Differentiation

11.3.1. Euler Derivative

Computing a derivative numerically, is typically not difficult, but the accuracy of the calculation may be limited by the sampling rate of the data or by the limits of the computer to process very small numbers.

Calculus defines the derivative of y(x) with respect to x as

\frac{dy(x)}{dx} = \lim_{\Delta\,x \rightarrow 0} \frac{\Delta\,y(x)}{\Delta\,x}.

For discretely sampled data, this becomes an approximation.

\frac{dy_i}{dx} \approx \frac{y_{i+1} - y_i}{h}

The variable h represents the distance between the samples with respect to x (\delta x) and is proportional to the error, which may be acceptable for some applications, but not acceptable for other applications. This algorithm is called the forward Euler finite-difference derivative.

For sampled data values, the MATLAB function diff returns the difference between consecutive values, dy_dx = diff(y)/h;. Note that the size of the array returned by diff is one element smaller than the array passed to it.

To take the derivative of a function, first sample the data at intervals of h; and then use diff as with pre-sampled data. The challenge is to determine an appropriate value for h. It should be small enough to give good granularity. The evaluation of small enough depends entirely on the data being evaluated. However, it should not be so small as to require excessive computation or to cause excessive rounding errors from the division by h. As a rule of thumb, h should not be much smaller than 10^{-8}. Some testing of different values of h may be required for some applications.

Try this example code and see how changing the value of h, affects the accuracy of the numerical derivative. Fig. 11.9 shows the plot when h = \pi/40.

% File: deriv_cos.m
% Derivative example, Compute derivative of cos(x)

% sample step size, please experiment with h values
h = pi/40;
x = 0:h:2*pi;
y = cos(x);
dy_dx = diff(y)/h;
x1 = x(1:end-1);      % note one less to match dy_dx
actual_dy = -sin(x1);
error = abs(dy_dx - actual_dy);
me = max(error);
ex = x1(error == me);

p1 = plot(x1, actual_dy, 'k', x1, dy_dx, 'r:');
title('Derivatives of cos(x)');
xticks(0:pi/2:2*pi);
xticklabels({'0','\pi/2','\pi','3\pi/2','2\pi'});
line([ex ex], [-1 1]);
text(ex+0.1, -0.4, 'Max error location');
legend(p1,{'analytic derivative','numerical derivative', },...
    'Location', 'northwest');
disp(['Max error = ',num2str(me)]);
../_images/deriv_cos.png

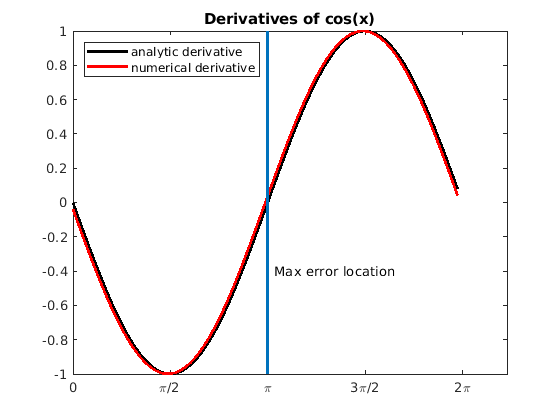
Fig. 11.9 Even though the h value is fairly, the numerical derivative of the cosine function is close to the analytical derivative.

11.3.2. Spectral Derivative

The fast Fourier transform (FFT) provides a more accurate numerical method for estimating a derivative. The Fourier series, Fourier transform, and the inverse Fourier transform are algorithms proposed in 1807 by French mathematician Jean Baptiste Joseph Fourier (1768-1830) to characterize the frequencies present in continuous functions or signals. Later, the discrete Fourier transform (DFT) was used with sampled signals; however, the DFT can be rather slow for large data sets (\mathcal{O}(n^2)). Then in 1965, James W. Cooley (IBM) and John W. Tukey (Princeton) developed the fast Fourier transform (FFT) algorithm that has run-time complexity of \mathcal{O}(n\,\log{}n). The improved performance of the FFT stems from taking advantage of the symmetry found in the complex, orthogonal basis functions (\omega_n = e^{-2\pi i/n}). I will resist the temptation to go into a detailed description of the Fourier transform and the FFT. Many other resources cover that. For a fairly simple explanation, see my Machine Vision Study Guide, which emphasis the 2-D FFT used with images. A more rigorous, but still understandable coverage can be found in [BRUNTON19], pages 47 to 63.

The FFT is of interest to us here because of the simple relationship between the Fourier transform of a function and the Fourier transform of the function’s derivative. We can easily find the derivative in the frequency domain and then use the inverse FFT to put the derivative into its original domain.

\mathcal{F}(df/dt) = i\,\omega\,\mathcal{F}(f)

Here, i is the imaginary constant \sqrt{-1} and \omega is the frequency in radians per second for time domain data or just radians for spatial data. We can use \omega = 2\pi f_s k/n for time domain data and \omega = 2\pi k/T for spatial domain data, where k is the sample number in the range -n/2 \to (n/2 - 1), n is the number of data samples (usually a power of 2), f_s is the sampling frequency (samples/second), and T is the total length of the spacial domain data.

The following example is derived from Brunton’s book on data science and engineering [BRUNTON19], pages 62 - 63, with a few modifications for clarity. The example uses one dimensional, spatial domain data. The example shows how the spectral derivative aligns with the analytic derivative. The FFT shows frequency data as having both negative and positive frequencies, so our \omega needs to split the range of frequencies between the negative and positive. For this example, we want to examine the function and derivative at negative and positive values, so we can use our k variable to build both the spatial x values and the frequency w values. Both the FFT and inverse FFT algorithms reorder the data, so we need to use the fftshift function to align the frequency values with the frequency data.

%% SpectralDerivative.m
%  Numerical derivative using the spectral derivative (FFT based)
%  algorithm. Based off code from "Data Driven Science and
%  Engineering" by Burnton and Kutz.

n = 128;
L = 15;         % x data from -15 to 15
T = 2*L;
k = -n/2:(n/2 - 1);
x = T*k/n;
f = cos(x).*exp(-x.^2/25);                    % Function
df = -(sin(x).*exp(-x.^2/25) + (2/25)*x.*f);  % Derivative

%% Derivative using FFT (spectral derivative)
fhat = fft(f);
w = pi*k/L;           % radians, 2*pi*k/T = pi*k/L
omega = fftshift(w);  % Re-order fft frequencies
i = complex(0, 1);    % Define i just to be sure it is not used for
                      % something else, or could use 1i.
dfhat = i*omega.*fhat;
dfFFT = real(ifft(dfhat));

%% Plotting commands
figure, hold on
plot(x, f, 'b')
plot(x,df,'k','LineWidth',1.5)
plot(x,dfFFT,'r--','LineWidth',1.2)
legend('Function', 'True Derivative','FFT Derivative')
hold off
../_images/spectralDerivative.png

Fig. 11.10 Example spectra derivative compared to the analytic derivative

Here is an example of computing the spectral derivative using time domain data. Fig. 11.11 shows a plot of spectral time domain derivative, which aligns with the analytic derivative.

%% SpectralTimeDerivative.m
%  Numerical derivative using the spectral derivative
%  (FFT based) algorithm --  time domain data
n = 256;
fs = 8000;          % samples/second
T = n/fs;           % time span of samples (seconds)
k = -n/2:(n/2 - 1);
t = T*k/n;          % time values
f1 = 200;           % Two frequency components
f2 = 500;

f = 2*cos(2*pi*f1*t) + cos(2*pi*f2*t);                  % Function
df = -4*f1*pi*sin(2*pi*f1*t) - 2*f2*pi*sin(2*pi*f2*t);  % Derivative

%% Derivative using FFT (spectral derivative)
fhat = fft(f);
w = 2*pi*fs*k/n;      % radians / second
omega = fftshift(w);  % Re-order fft frequencies
i = complex(0, 1);    % Define i just to be sure it is not used for
                      % something else, or could use 1i.
dfhat = i*omega.*fhat;
dfFFT = real(ifft(dfhat));

%% Plotting commands
figure, plot(t, f, 'b')  % derivatives too large for same plot
title('Function'), xlabel('seconds');
figure, hold on
plot(t, df,'k','LineWidth',1.5)
plot(t, dfFFT,'r--','LineWidth',1.2)
legend('True Derivative','FFT Derivative')
title('Derivatives'), xlabel('seconds');
hold off

%% Plot the power spectrum
pwr = abs(fhat).^2/n;
figure, plot(omega/(2*pi), pwr);
xlim([-800 800])
xlabel('Frequency (Hz)'), ylabel('Power'), title('Power Spectrum')
../_images/spectralTimeDeriv.png

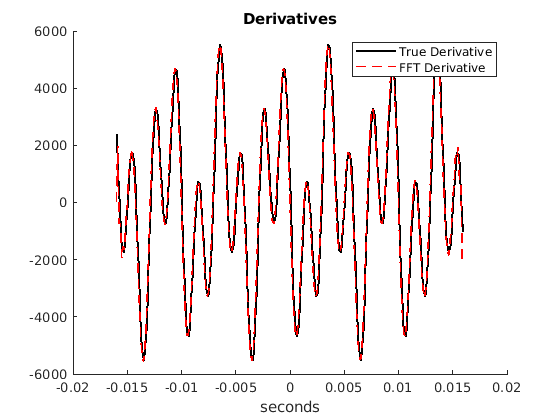
Fig. 11.11 Plot of the analytic derivative and spectral derivative of a time domain signal.