4.5. Generating Random Numbers

Random numbers are useful for creating simulations, and to emulate the presence of noise or random chance. MATLAB includes continuous and discrete random number generators for uniform and normal distributions. Random number generators for a different probability distributions can be derived from the uniform and normal generators. The Statistics and Machine Learning Toolbox has random number generators for other distributions. A search on the Internet will find source code for random number generators for other distributions.

rng

All MATLAB random number generating functions can be seeded to generate either a repeatable or unique sequence of pseudo-random numbers with the rng function. Seeding the random number generator with a fixed number results in the same sequence of numbers, which is helpful for comparisons of algorithms and is a debugging strategy because runs are reproducible. A strategy to get a unique sequence each time a program runs is to use the current time as the seed number with rng("shuffle"). See the rng documentation.

rand

The rand(n) function creates a n{\times}n matrix of uniformly distributed random numbers in the interval (0 to 1). rand(m, n) creates a m{\times}n matrix or vector. To generate n random numbers in the interval (a, b) use the formula r = a + (b-a)*rand(1, n). A uniform distribution means that each number is equally likely. See the rand documentation.

randn

The randn function creates random numbers with a normal (Gaussian) distribution. The parameters to randn regarding the size of the returned data is the same as for rand. The values returned from randn have a mean of zero and variance of one. To generate data with a mean of a and standard deviation of b, use the equation y = a + b*randn(N,1). See randn documentation, and Random Numbers from Normal Distribution with Specific Mean and Variance. See information about the normal distribution.

randi

The randi(Max, m, n) function creates a m{\times}n matrix of uniformly distributed random integers between 1 and a maximum value. Provide the maximum value as the first input, followed by the size of the array. randi documentation

randperm

The randperm function returns a row vector containing a random permutation of the integers from 1 to n without repeating elements. One application of this is to achieve a shuffle operation, like with a deck of playing cards. randperm documentation.

Histograms of each random number generator is shown in Fig. 4.8.

% File: randGenPlots.m
t = tiledlayout(3, 1);
title(t, 'Random Number Generators')
nexttile;
histogram(20*rand(1, 1000), 40)
title('rand \sim U(0, 20)')
nexttile;
histogram(randi(20, 1, 1000), 20)
title('randi \sim U(1, 20) integers')
nexttile;
histogram(10 + 3*randn(1, 1000), 40)
title('randn \sim N(10, 3)')
../_images/RandGens.png

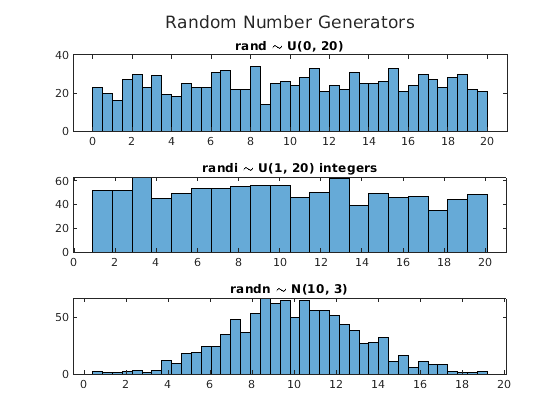
Fig. 4.8 Histograms of random number generators

4.5.1. Exponential Random Number Generator

Recall from Continuous Distributions that (4.1) is the CDF of the exponential probability distribution.

(4.1)F(a) = \left\{ \begin{array}{ll} 1 - e^{-\lambda\,a}, &a > 0 \\ 0, &a \leq 0 \end{array} \right.

Equation (4.2) shows the inverse of the CDF found by letting y = F(a) and solving for a. To make an exponential random number generator we use (4.2) and the rand number generator that has a uniform distribution in the interval (0, 1). Fig. 4.9 shows a histogram of a random variable created with our random number generator.

(4.2)a = F^{-1} = \frac{1}{\lambda}\,\ln\left(\frac{1}{1 - y}\right)

function X = randexp(lambda, m, n)
% RANDEXP - Simple exponential distribution random
%    number generator. If you have the Statistics
%    and Machine Learning Toolbox, use exprnd.
%
% lambda - exponential distribution parameter
%   mean(X) ~ 1/lambda, var(X) ~ 1/lambda^2
%   Output is size m x n
    y = rand(m, n);      % y ~ U(0, 1)
    y(y == 1) = 1 - eps; % protect from divide by 0
    X = log(1./(1-y))./lambda; % inverse of CDF
end

>> X = randexp(2.0, 1, 500);
>> x_bar = mean(X)
x_bar =
    0.5005
>> s2 = var(X)
s2 =
    0.2887
>> histogram(X)
../_images/expHist.png

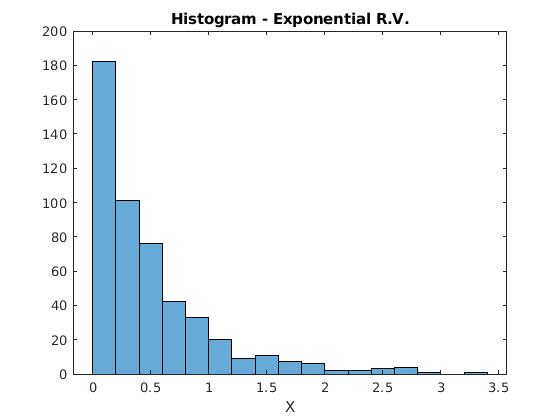
Fig. 4.9 Histogram from the exponential random number generator

4.5.2. Monte Carlo Simulation

Here is a fun application of a random number generator. It performs what is called a Monte Carlo simulation to make a good estimate the value of \pi [GUTTAG16]. This is done by creating a set of uniform distributed random points in a square between -1 and 1 in both the x and y directions. Then we relate the ratio of the number of points that fall inside a circle of radius 1 to the total number of points. The number of points inside the circle should be related to the area of the circle. Since the sides of the square is 2, the area of the square is 4, while the area of the unit circle is \pi. A plot of the points inside and outside of the circle is shown in Fig. 4.10.

% File: randpi.m
% Script to use a random number generator to estimate the value of PI.
% This is an example of a Monte Carlo simulation.

N = 1000000;

% 2-D points on a plane, uniform distribution in each dimension
% between -1 and 1.
points = 2*rand(2, N) - ones(2, N);
% scatter(samples(1,:), samples(2,:), '.')
radii = vecnorm(points);    % distance of each point from (0, 0).
inCircle = radii <= 1;      % logical vector of points inside circle

% Area of square is 4. Area of circle is pi. So the ratio of points
% inside the circle to the total should be pi/4.
piEstimate = 4*nnz(inCircle)/N;
error = 100*abs(piEstimate - pi)/pi;
disp(['Estimate of pi is: ', num2str(piEstimate)])
disp(['The error was ', num2str(error), ' percent.'])

% plot the points inside and outside of the circle.
figure, axis equal
hold on
scatter(points(1, inCircle), points(2, inCircle), '.')
scatter(points(1, ~inCircle), points(2, ~inCircle), '.')
hold off
title('Monte Carlo Estimate of \pi')
../_images/monteCarlo.png

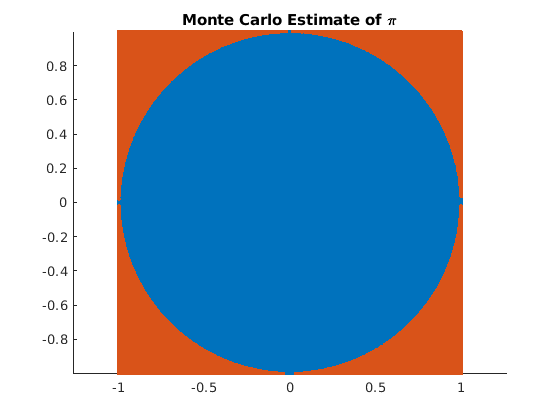
Fig. 4.10 The ratio of points inside the circle to total points is close to \pi/4.

4.5.3. Random Casino Walk

Another use of random number generators is a random walk simulation. Random walks represent a cumulative series of random numbers that at each step can move the state of the simulation. Random walks can be performed in different dimensions. In the example here, the dimension of the random walk is one.

This is a simulation of playing slot machines at a casino. One hundred players each start with 80 quarters ($20). Each player plays all 80 quarters and counts their winnings at the end. The machines are programmed to return 80% of what they take in. So the expected winnings of each player is $16 after spending $20 (loss of $4). Sometimes the machines give winners 4 quarters and sometimes they payout 8 quarters.

Logical arrays simplify the implementation. We use integer random numbers with a uniform distribution for events with simple percentages of occurrence. A histogram of the winnings for the 100 players is shown in Fig. 4.11. The shape of the histogram also affirms the central limit theorem described in Central Limit Theorem.

% File: casinoWalk.m
% Random walk simulation of playing slot machines.
% 100 people each start with 80 quarters ($20).
% They play all 80 quarters and see how much money they
% have in winnings. The slot machines payout 80% of
% what they take in. Half of the time they use 1/5 odds
% to pay 4 quarters. The other times they use 1/10 odds
% to pay 8 quarters. You should find the average winning
% to be about -4 dollars.

winning = zeros(1, 100);
for p = 1:100   % for each player
    oneIn10 = randi(2, 1, 80) == 2; % win 1/10 or 1/5
    rand = randi(10, 1, 80);
    payout = zeros(1, 80);
    payout(oneIn10 & rand == 10) = 8;
    payout(~oneIn10 & rand > 8) = 4;
    winning(p) = sum(payout)/4 - 20; % net winnings
end
disp(['Average winning = $', num2str(mean(winning))])
histogram(winning, 25)
xlabel('Winnings ($)')
ylabel('Players out of 100')
title('Slot Machine Net Winnnings on $20')
../_images/slots.png

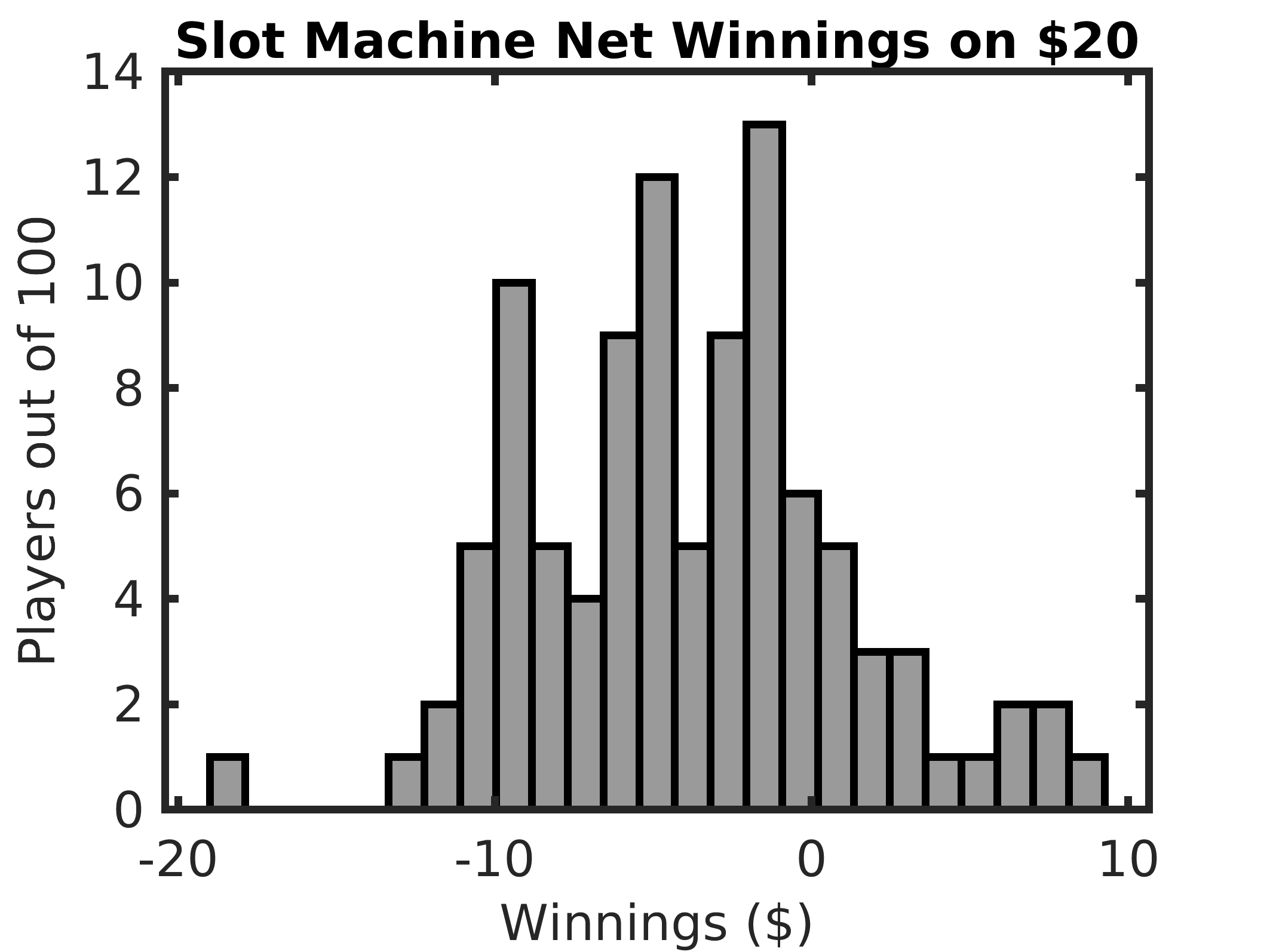
Fig. 4.11 Histogram of winnings after $20 on slot machines.