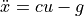2.1. System Plant Models¶
The dynamics of the system is the called the system plant. The system plant is why we need a controller. The plant is the result of mechanical inefficiencies and forces on the system such as gravity and friction. The system plant usually varies with time, such as when a car goes up and down hills as it travels along a road, or when a mobile robot moves from a smooth concrete floor to a carpeted floor. A poor way to design a controller is to try tuning the controller parameters purely from observation. A better approach is to first model the plant’s physics and environment. An understanding of the plant can help determine the basic strategy and needed elements of the controller. Then simulation software, such as Simulink, can be used for initial tuning of the parameters. Of course, final tuning and verification of the correctness of the system plant model may require testing and observations from the actual system.
2.1.1. Cruise Control¶
A common way to model a system is to consider the forces acting on the
system. This is the approach used to model a cruise controller for a car.
The amount of gas supplied to the engine is modeled as a force 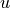 ,
which is the output from the controller. Another force is wind drag, which
is proportional to the velocity. Rolling inefficiency is considered to be
offset by the car’s momentum.
,
which is the output from the controller. Another force is wind drag, which
is proportional to the velocity. Rolling inefficiency is considered to be
offset by the car’s momentum.
The input to the simulation is a step function modeling that the car is to go from being stopped to moving at a specified speed. The output velocity is calculated as the integral of the acceleration.

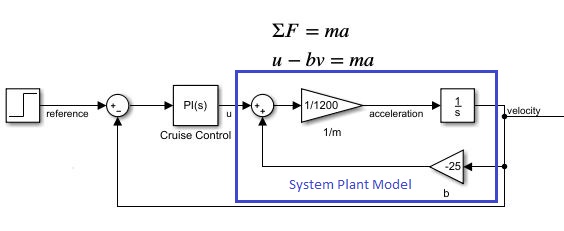
Fig. 2.2 Simulink model of a car with cruise control¶
2.1.2. UAS Altitude Control¶
If the altitude of a quadrotor UAS is given by 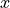 , the system model
might want to consider acceleration, which is the second derivative of
, the system model
might want to consider acceleration, which is the second derivative of
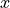 ,
, 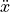 . This makes sense because the main external
force is gravity, which is an acceleration. We can measure the altitude of
the system and use derivatives to find both the vertical velocity and
acceleration.
. This makes sense because the main external
force is gravity, which is an acceleration. We can measure the altitude of
the system and use derivatives to find both the vertical velocity and
acceleration.