17.6. FFT Agorithm

In MATLAB, and almost any other computer environment, when we want to compute the DFT, we use a function called fft() for the 1D-DFT, fft2() for the 2D-DFT, and likewise ifft(), and ifft2() for the inverse transforms. The result of using these functions for the DFT and inverse DFT is exactly the same as computing a DFT using the DFT equations. FFT stands for Fast Fourier Transform. FFT is a computer programming algorithm to compute the DFT with a fewer number of calculations as the normal DFT equation would suggest. 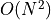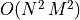The normal computational complexity for the 1D-DFT and 2D-DFT is O(N^2) and O(N^2\,M^2). 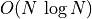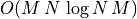The FFT algorithm computes the DFTs with complexity O(N\,\log N) and O(M\,N\,\log N\,M). The FFT algorithm is faster because it uses symmetry of the complex exponential basis function to quickly determine most of the basis function values from other previously known values.

For this course, we are interested in using the fft2() and ifft2() that are built into MATLAB. We do not need to study exactly how the algorithm works.

Note

There is one important matter to be aware when using the FFT algorithm to compute DFTs. The size of the data set processed in each dimension should ideally be a power of 2. The are two reasons for this. First, the algorithm works faster when the length is a power of 2 because it repeatedly splits the basis functions in half to quickly calculate the basis function values. Secondly, the frequency resolution, and thus the results, are more accurate when the length is a power of 2. Many experts suggest that when the length is not a power of 2 that zeros should be added to make the data a power of 2 in length. The images that we work with for the course will all have power of 2 sizes, so we won’t have to worry about it. Here is a web page that discusses this.