10.4. Stereo Cameras¶

Reading Assignment

Please review chapter 14 of [RVC], which gives a much broader coverage of the general topic of using multiple images than we cover here.

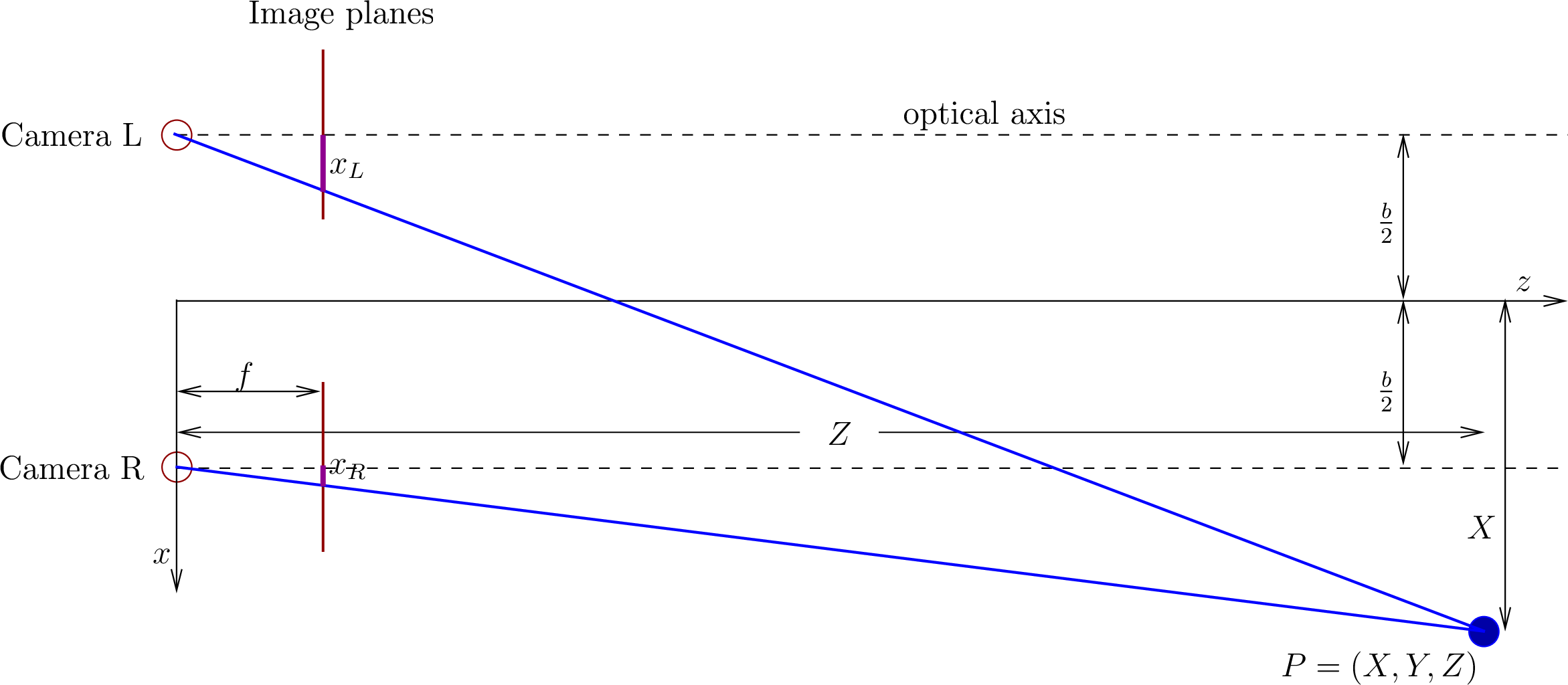
One way to obtain the distance of objects from the camera (variable 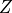$Z$ ), is to use two cameras in a Parallel axis stereo camera system. An example of such a system is the Bumblebee from FLIR (Point Grey).

The first step is to find the locations, called corresponding points, of the same point in the two images. The same point in the two images are always found on the same epipolar line. The epipolar line is the line on each image where the epipolar plane intersects the image plane. Finding the epipolar line for cameras without parallel optical axes is quite a bit harder than the problem that we will consider here. Algorithms to find sets of corresponding feature points, such as the RANSAC and SURF, are first used.

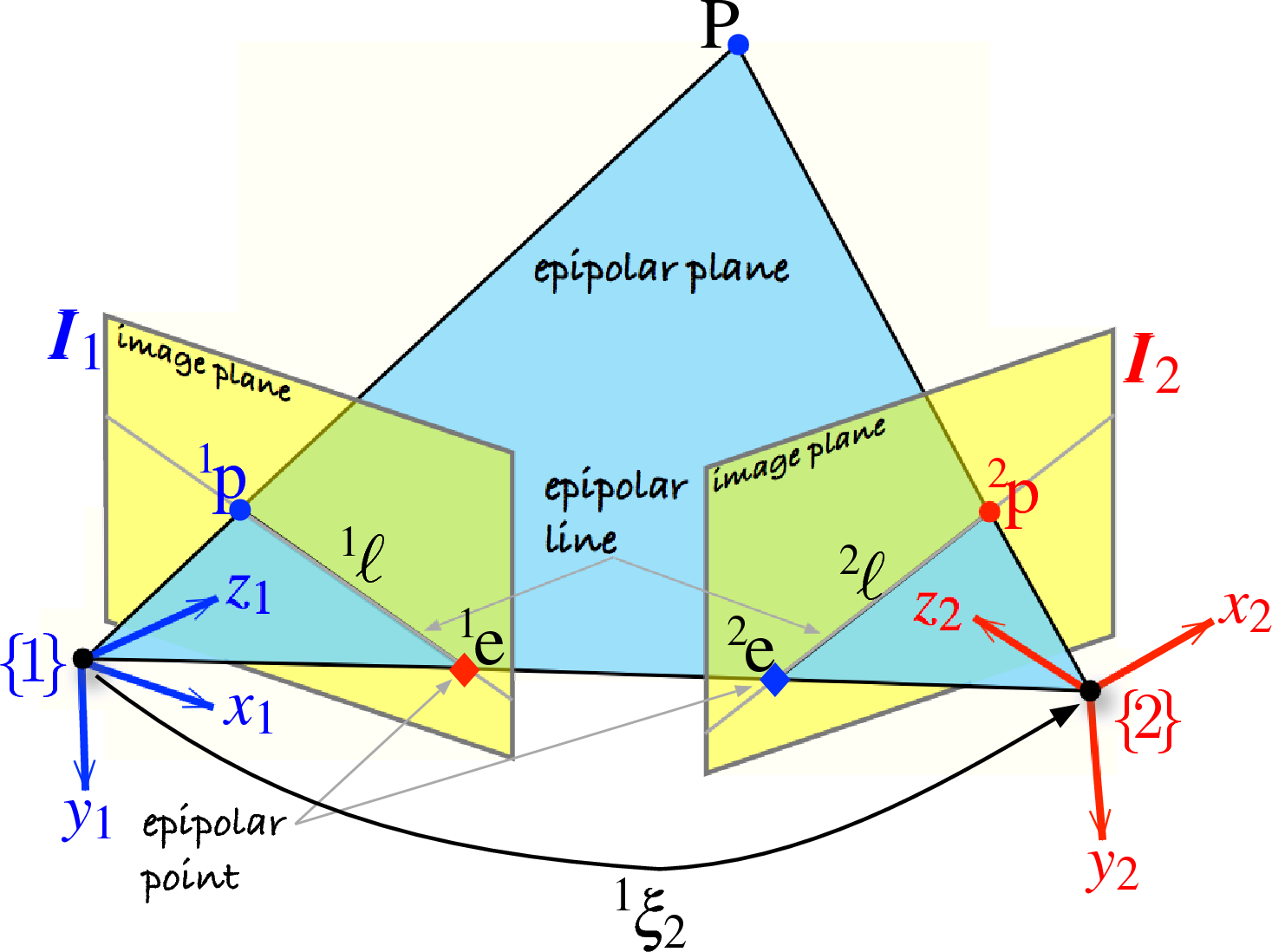
Figure 14.5 from [RVC].

epipolar plane: The epipolar plane is the triangular plane formed between the origins of the two cameras and a point in the physical world captured by the two images.

For parallel axis stereo cameras, the epipolar lines are simply lines with a constant $v$ . Thus to find corresponding points, we simply look for a corresponding point in the right image to left of the point in the left image along the line with the same $v$ .

The coordinate frame for the system can be either placed at the left camera or at the center point between the cameras. Here, I used the center point. The distance between the optical axis of the cameras is 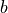$b$ .

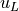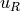The pixel locations along the x-axis in the images are $u_L$ and $u_R$ . From the perspective projection equation:

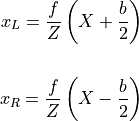
$x_L = \frac{f}{Z}\left(X + \frac{b}{2}\right) \\ x_R = \frac{f}{Z}\left(X - \frac{b}{2}\right)$

We find what is called the disparity by taking the difference:

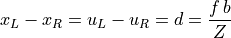
$x_L - x_R = u_L - u_R = d = \frac{f\,b}{Z}$

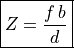
$\boxed{Z = \frac{f\,b}{d}}$

Objects that are close to the camera have a larger disparity than objects further away. This can be confirmed with a quick experiment using your two eyes. Place two objects in front of you with one further away than the other. Do not move your head during the experiment. Hold your hand over your right eye and note the relative position of the objects as seen with your left eye. Quickly switch so that your left eye is covered and view the objects with your right eye. Note how your view of the positions of the objects changes depending on which eye you are using. You should see that your view of the closer object shifts more than your view of the further object.

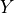The $X$ and $Y$ position of a point may be found from either the left or right image. The left image is usually used. The $X$ and $Y$ position are calculated with respect to the optical axis.

If the image has M rows and N columns ([M, N] = size(im)), then we can find the center of the image:

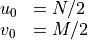
$\begin{array}{ll} u_0 &= N/2 \\ v_0 &= M/2 \end{array}$

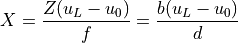
$X = \frac{Z (u_L - u_0)}{f} = \frac{b (u_L - u_0)}{d}$

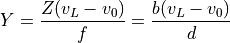
$Y = \frac{Z (v_L - v_0)}{f} = \frac{b (v_L - v_0)}{d}$

Note

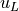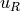A prerequisite to finding the depth of points from the images is to match coorseponding points ( $u_L$ and $u_R$ ) between the images. That is a different topic than discussed here.

The Machine Vision Toolbox has some functions that can be used to find depth from stereo images.

stdisp( L, R )

Displays the stereo image pair L and R in adjacent windows to manually find the disparity between points in the images.

Two cross-hairs are created. Clicking a point in the left image positions black cross hair at the same pixel coordinate in the right image. Clicking the corresponding world point in the right image sets the green crosshair and displays the disparity [pixels].

D = istereo(LEFT, RIGHT, RANGE, H, OPTIONS)

Computes a disparity image computed from the epipolar aligned stereo pair: the left image LEFT (HxW) and the right image RIGHT (HxW). D (HxW) is the disparity and the value at each pixel is the horizontal shift of the corresponding pixel in IML as observed in IMR. That is, the disparity d=D(v,u) means that the pixel at RIGHT(v,u-d) is the same world point as the pixel at LEFT(v,u).

RANGE is the disparity search range, which can be a scalar for disparities in the range 0 to RANGE, or a 2-vector [DMIN DMAX] for searches in the range DMIN to DMAX.

H is the half size of the matching window, which can be a scalar for NxN or a 2-vector [N,M] for an NxM window.

% Images from the Middlebury Stereo Database
% f/rho = 3989 pixels, baseline = 193 mm

%%
fb = 3989*0.193;
% b = 0.193; % meters

L = iread('im0.png', 'reduce', 2, 'double', 'grey');
R = iread('im1.png', 'reduce', 2, 'double', 'grey');
% stdisp(L, R)
d = imgaussfilt(istereo(L, R, [20, 110], 3), 5);

iZ = fb./d;
figure
idisp(iZ, 'colormap', jet(246), 'bar')

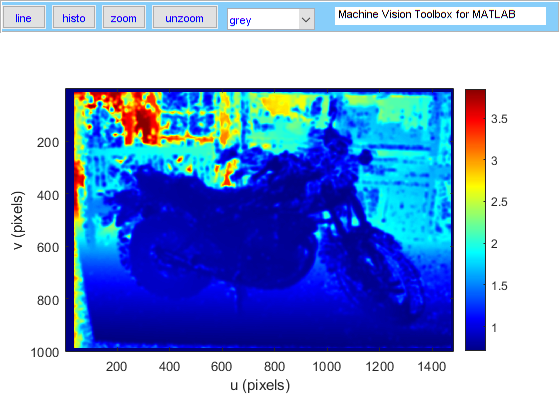
Output estimating depth from stereo camera images

10.4. Stereo Cameras¶

Previous topic

Next topic

This Page