10.1. Cameras¶
The original optical cameras used a small hole (pin hole) on the side of a dark room. The inverted object was projected on the opposite wall (the image plane).

Figure 11.1a from [RVC], Pin Hole camera.
10.1.1. Camera Lenses¶
Pin hole cameras are always in focus, but the amount of light that projects on the image plane is insufficient. Lenses increase the amount of light that projects on the image plane, but the geometry of the camera needs adjustments for the image to be focused on the image plane.
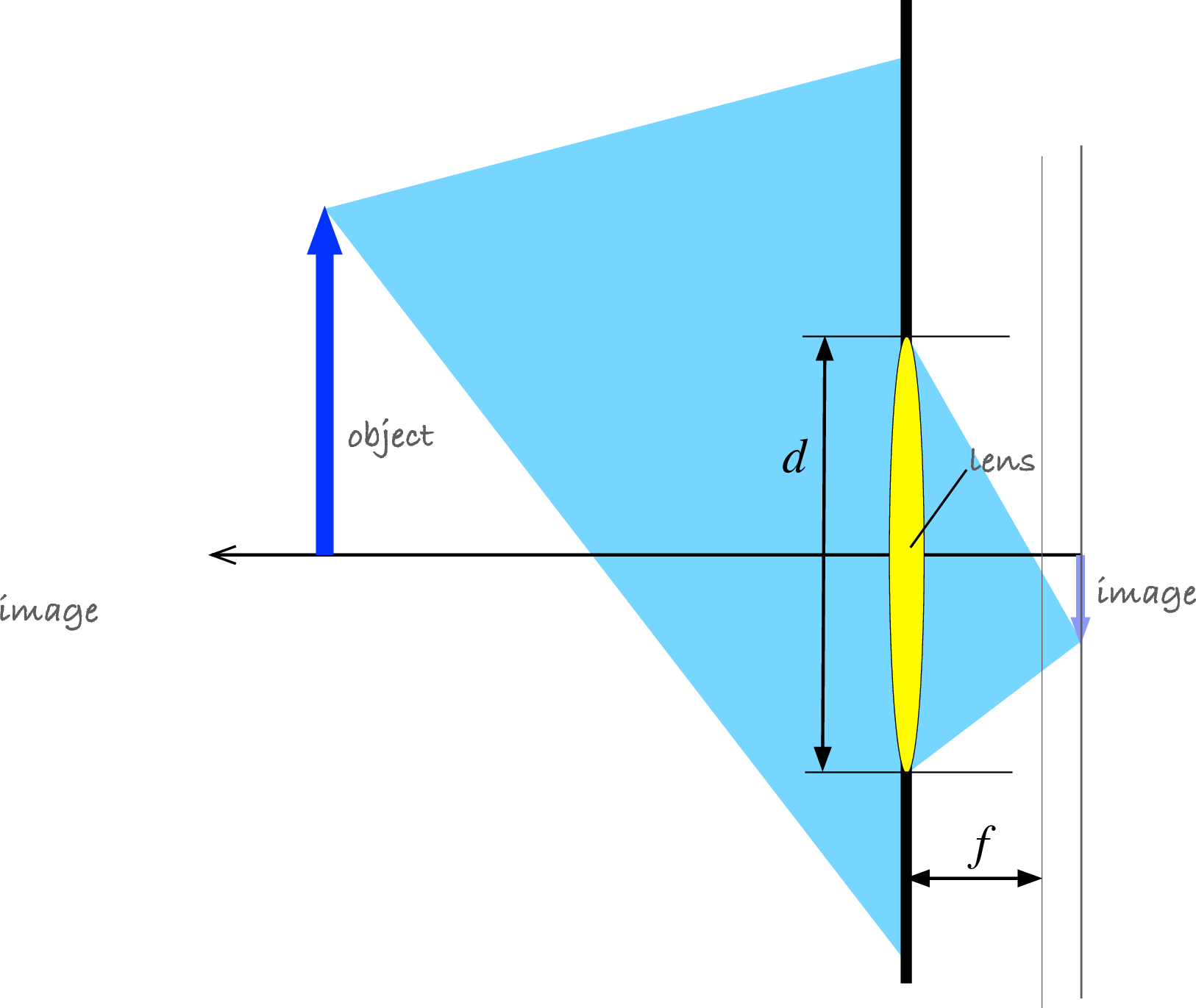
Figure 11.1b from [RVC], lenses allow more light to project onto the image plane with the penalty that focusing is required to clearly see objects of interest.
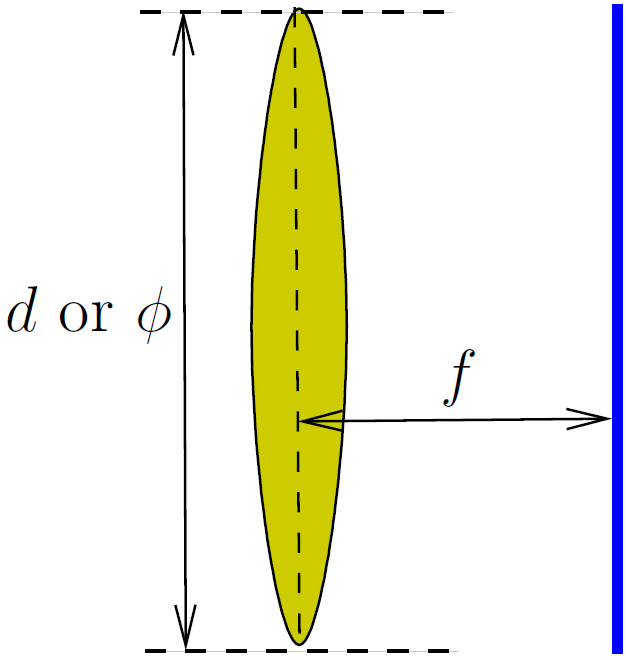
A measure of how much light the lens projects on the image plane is the F-Number. The F-number is often printed on the camera lens. It is the ratio of focal length to the diameter of the lens. A smaller F-number lens results in a brighter image (more light) than produced from a lens with a larger F-number.
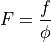
10.1.2. Thin Lens Camera Model¶
Although cameras are often more complex, the simplified thin lens camera
model does a nice job of modeling the zoom and focus of a camera. In this
model, 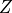 represents the distance from the camera to the photographed
object;
represents the distance from the camera to the photographed
object; 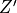 is the distance inside the camera from the lens to the image
plane;
is the distance inside the camera from the lens to the image
plane; 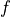 is the focal length of the lens.
is the focal length of the lens.
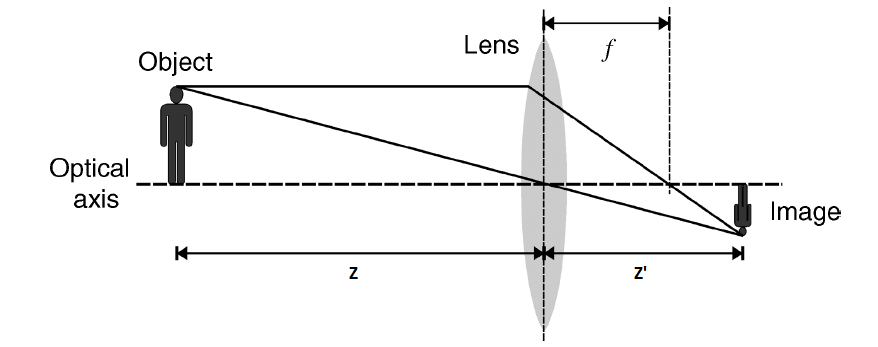
Thin Lens Camera Model
Using similar triangles and some algebra, we get the thin lens equation.
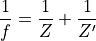
Optical zoom is achieved by changing the focal length, 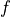 , The longer
the focal length, the narrower the angle of view and the higher the
magnification. The shorter the focal length, the wider the angle of view and
the lower the magnification. Objects are brought into focus by adjusting
, The longer
the focal length, the narrower the angle of view and the higher the
magnification. The shorter the focal length, the wider the angle of view and
the lower the magnification. Objects are brought into focus by adjusting
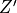 . Objects in focus on the image plane when the thin lens equation is
satisfied.
. Objects in focus on the image plane when the thin lens equation is
satisfied.
-
Example What value of
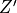 will bring an object 2 meters from the camera
into focus when
will bring an object 2 meters from the camera
into focus when 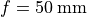 ?
?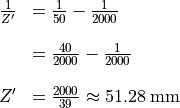
10.1.3. Lens Distortions¶
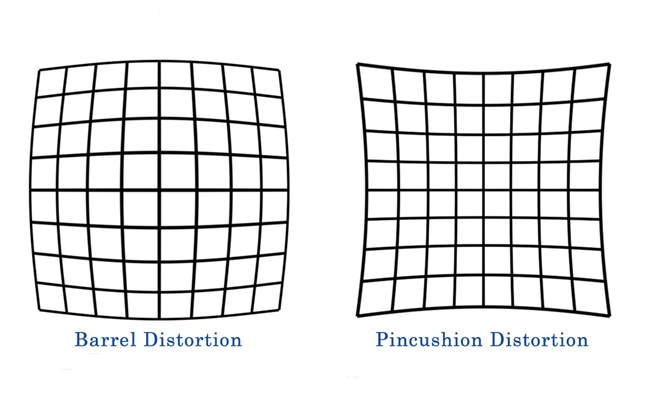
Most camera lens are not perfect. Images from a camera may exhibit geometric distortions such as barrel distortion or pincushion distortion as pictured below. Chromatic aberrations cause extra red colors to appear especially at the edge or fringe of objects. Vignetting results in dark corners of an image.
Lens distortions can sometimes be corrected with software. They can be mostly avoided by buying an expensive lens. The diagram below shows all of the lens in a Nikon 24-70 mm zoom lens that is designed to not have any distortions. The cost for such a lens is about $1,500 in 2023.