9.2. How SVD Changes Vectors¶
Except for rotation matrices and eigenvectors, we normally see rotation
and stretching when a vector is multiplied by a matrix. When the matrix
is represented by its SVD factors, we see rotation, stretching, and
again rotation when we multiply a vector sequentially by
\(\mathbf{V}^T\), \(\mathbf{\Sigma}\), and \(\mathbf{U}\).
Use the demonstration function showSVD to experiment with several
\(2{\times}2\) matrices to see the rotation, stretching, and second
rotation. The demonstration starts with a set of points on a circle.
Ultimately, the circle pattern will be changed to show a rotated
ellipse. Figure Fig. 9.4, and figure
Fig. 9.5 show example plots. The plots will be
different for each matrix supplied.
function show_SVD(A)
% SHOW_SVD - A demonstration of how the U, S, and V matrices
% from SVD rotate, stretch, and rotate vectors making a circle.
% Try several 2x2 matrices to see how each behaves.
theta = linspace(0, 2*pi, 30); x = [cos(theta); sin(theta)];
[U,S,V] = svd(A); Vx = V'*x;
figure, plot(x(1,:), x(2,:), '*')
hold on, scatter(Vx(1,:), Vx(2,:))
for z = 1:30
line([x(1,z), Vx(1,z)], [x(2,z), Vx(2,z)], 'Color', 'k')
end
hold off, title('Rotation by V^T Matrix')
svx = S*Vx;
figure, scatter(svx(1,:), svx(2,:), '*')
daspect([1 1 1]), usvx = U*svx;
hold on, scatter(usvx(1,:), usvx(2,:), 'o'), hold off
title('Stretch by \Sigma and rotation by U')
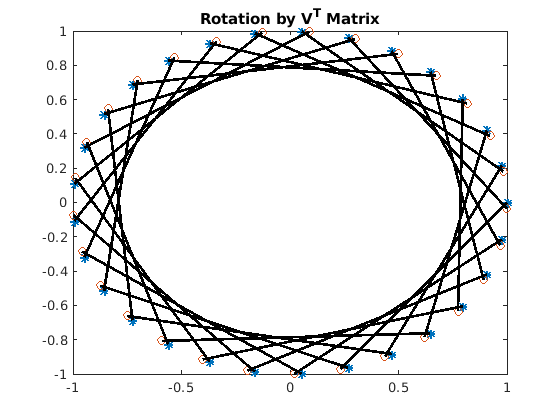
Fig. 9.4 When each point is multiplied by \(\mathbf{V}^T\) the points rotate around the circle. The lines show the initial and final positions of the points.¶
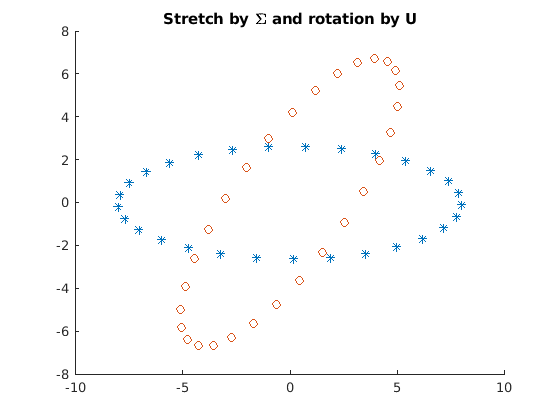
Fig. 9.5 When each point is multiplied by \(\mathbf{\Sigma}\), the points around the circle are moved out from the center to form an ellipse. Then the ellipse is rotated when the points are multiplied by \(\bf{U}\).¶
