12.4.3. Direct Algorithms¶
Direct algorithms have a pre-determined number of steps based on the
data size. However, the number of calculations of iterative algorithms
is non-deterministic. Three algorithms step down the matrix diagonal,
applying a sequence of Householder reflections. The QR decomposition is
used in eigendecomposition algorithms as described in Iterative QR Algorithm,
but it is also used to solve systems of linear equations
(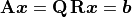 ). The Hessenberg and
bidiagonal decompositions are preliminary steps to iterative algorithms
to find the eigendecomposition and the SVD.
). The Hessenberg and
bidiagonal decompositions are preliminary steps to iterative algorithms
to find the eigendecomposition and the SVD.
12.4.3.1. QR Decomposition¶
The MATLAB command, [Q, R] = qr(A)
finds the factors 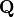 and
and 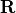 of
of 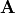 .
The function
.
The function qrFactor listed below is a simple
algorithm implementation. It does not handle under-determined matrices,
nor is it as flexible or as robust as MATLAB’s qr function. The
qrFactor function makes use of the householder function
to compute the Householder reflection matrices that,
with multiplication, convert 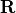 to upper triangular
form. [1] Then, the
to upper triangular
form. [1] Then, the 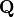 matrix is built as an orthogonal
product of transposed reflection matrices. The code is based on
pseudo-code in Demmel’s Applied Numerical Linear Algebra
text [DEMMEL97] and Golub and Van Loan’s Matrix
Computations text [GOLUB13].
matrix is built as an orthogonal
product of transposed reflection matrices. The code is based on
pseudo-code in Demmel’s Applied Numerical Linear Algebra
text [DEMMEL97] and Golub and Van Loan’s Matrix
Computations text [GOLUB13].
function [Q, R] = qrFactor(A, econ)
% QRFACTOR - Simple QR factorization using Householder reflections.
% [Q, R] = QRFACTOR, yields Q and R factors such that A = Q*R.
%
% A - input real or complex m-by-n matrix, (m >= n).
% econ - (optional) enter 0 (zero) to get the economy QR,
% where Q is m-by-n and R is n-by-n. [Q, R] = qrFactor(A, 0);
% Q - Unitary basis vectors of A (m-by-m)
% R - Upper triangular matrix (m-by-n)
%
% See also: QR, EIGQR, SVDQR, HOUSEHOLDER
%
[m, n] = size(A);
if m < n
error('Matrix must be square or over-determined')
end
R = A;
Q = eye(m);
for k = 1:min((m-1), n)
H = householder(R(k:m, k), m, k-1);
R = H*R;
R(k+1:m,k) = zeros(m-k,1); % no round-off error
Q = Q*H';
% For real numbers H = H', but not in the complex case
end
% The econ option is useful with rectangular matrices.
if exist('econ','var') && econ == 0
Q = Q(:,1:n);
R = R(1:n, :);
end
end
12.4.3.2. Hessenberg Decomposition¶
The Hessenberg form [2] of a matrix has all zeros below the subdiagonal. [3] Householder transforms on each column clear the values below the subdiagonal. The algorithm uses similarity transformations to maintain the eigenvalues of the matrix (Similarity Transformations). To maintain the similarity, the transpose of the Householder transforms are multiplied from the right. The similarity requirement does not allow converting the matrix to upper triangular form with a direct calculation. The Hessenberg decomposition is as follows.
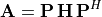
Note
When converted to Hessenberg form, a symmetric matrix becomes tridiagonal, where only the subdiagonal, diagonal, and superdiagonal hold nonzero elements.
MATLAB has a function called hess that converts a matrix to Hessenberg
form. The hessForm function shows an implementation of shifting a matrix to
Hessenberg form. In addition to returning the matrix in upper Hessenberg form,
the unitary matrix is also returned.
function [P, H] = hessForm(A)
% HESSFORM - Convert A to Hessenberg form using Householder reflectors.
% H = HESSFORM(A) is the Hessenberg form of the matrix A.
% The Hessenberg form of a matrix is zero below the first
% subdiagonal and has the same eigenvalues as A. If the matrix
% is symmetric or Hermitian, the form is tridiagonal.
%
% [P,H] = HESSFORM(A) produces a unitary matrix P and a Hessenberg
% matrix H so that A = P*H*P' and P'*P = EYE(SIZE(P)).
%
% A - input real or complex square matrix n-by-n.
[m, n] = size(A);
if m ~= n
error('Matrix must be square')
end
P = eye(n);
for k = 1:n-1
Hr = householder(A(k+1:m, k), m, k);
A = Hr*A*Hr';
A(k+2:m, k) = zeros(m-k-1, 1); % no round-off error
P = P*Hr';
% For real numbers H = H', but not in the complex case
end
if nargout<=1, P = A; else, H = A; end
end
12.4.3.3. Bidiagonal Decomposition¶
The bidiagonal decomposition is a preliminary step to the iterative algorithm
to calculate the SVD. A bidiagonal matrix is upper triangular, where the only
nonzero elements are on the diagonal and superdiagonal. The bidiagonal
decomposition of 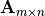 is given by
is given by 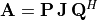 , where
, where 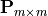 and
and
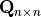 are orthogonal and
are orthogonal and
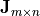 is bidiagonal. A sequence of Householder
transformations multiplied from the left and from the right convert the matrix
to bidiagonal form. Because similarity is not required, we design the
transforms multiplied from the right to set all row elements to the right of
the superdiagonal to zero. The function
is bidiagonal. A sequence of Householder
transformations multiplied from the left and from the right convert the matrix
to bidiagonal form. Because similarity is not required, we design the
transforms multiplied from the right to set all row elements to the right of
the superdiagonal to zero. The function bidiag implements the bidiagonal
decomposition.
function [P, J, Q] = bidiag(A)
% BIDIAG - Biagonal factoring of a matrix using Householder reflection
% transformations. Nonzero values are only along the main
% diagonal and the first superdiagonal.
%
% A - input real or complex matrix, square or over-determined (m-by-n)
%
% P - Pre-multiply transform
% J - bidiagonal of A - same singular values as A
% Q - Post-multiply transform
%
% A = P*J*Q'
%
% see also: HOUSEHOLDER, SVD65, SVD, svdFrancis
[m, n] = size(A);
if n > m % under-determined
error('Use the transform of under-determined matrices.')
end
P = eye(m); Q = eye(n);
J = A;
% Use Householder transformations to clear values below the main
% diagonal and to the right of the first superdiagonal.
for i=1:n-2
H = householder(J(i:m,i), m, i-1);
J = H*J; P = P*H'; J(i+1:m,i) = zeros(m-i,1);
H = householder(J(i,i+1:n)', n, i);
J = J*H'; Q = Q*H'; J(i,i+2:n) = zeros(1,n-i-1);
% For real numbers H = H', but not in the complex case
end
% last column of J to change for square matrix
H = householder(J(n-1:m,n-1), m, n-2);
J = H*J; P = P*H'; J(n:m,n-1) = zeros(m-n+1,1);
% last column of J for over-determined matrix
if m > n
H = householder(J(n:m,n), m, n-1);
J = H*J; P = P*H'; J(n+1:m,n) = zeros(m-n, 1);
end
if ~isreal(J)
% There are complex values at J(n-1,n) and J(n,n). We can
% only fix J(n,n).
H = eye(m); % make J(n,n) real
H(n,n) = conj(J(n,n))/abs(J(n,n));
J = H*J; P = P*H';
end
end % end of function
| [1] | Givens rotation transformations could be used by the QR algorithm instead of Householder transformations. |
| [2] | Karl Hessenberg (1904–1959) was a German electrical engineer and mathematician. He wrote the report where he introduced the Hessenberg form while he was a Ph.D. student at Technische Hochschule Darmstadt [HESSENBERG40]. |
| [3] | The subdiagonal is the diagonal below the main diagonal. |
