11.12. Homework 12 - Numerical Proof of Euler’s Formula

Note

The foundation of this assignment comes from math concepts that are very important to engineering. Some students may have previously been exposed to the math of this assignment. Probably some students have not worked with Euler’s formula before. This assignment demonstrates a numerical proof of Euler’s formula, which is a formula that can seem strange at first. It is hoped that having established a proof of the correctness of the formula using numerical methods will help students to understand this important formula.

11.12.1. Complex Numbers

A complex number contains both a real part and an imaginary part. The imaginary part is said to be a multiplied by the imaginary number, j = \sqrt{-1}.

C = a + j\,b

Mathematicians usually use the variable i as the imaginary number. Engineers, however, prefer to use the variable j.

One example of when we encounter complex numbers is when we solve for an unknown value to satisfy an equation. For example, the quadratic formula can be used to find values of x that satisfy a\,x^{2} + b\,x + c = 0. The two values of x are given by:

x = \frac{-b \pm\sqrt{b^{2} - 4\,a\,c}}{2\,a}

When 4\,a\,c > b^{2}, then x is a pair of complex conjugate numbers.

For this assignment, we will define a data structure to hold the real and imaginary parts of a complex number.

11.12.2. The Number e

See also

All About the Number e.

The number e \approx 2.7182818 is a very peculiar and important irrational number. It is defined using a limit.

e = \lim_{n\to\infty} (1 + 1/n)^n

and

e^x = \lim_{n\to\infty} (1 + x/n)^n, \forall x

Here are the limits of some exponentials that we already know about.

\begin{array}{ll} \lim_{n\to\infty} a^n = 0, & 0 < a < 1 \\ \\ \lim_{n\to\infty} a^n = 1, & a = 1 \\ \\ \lim_{n\to\infty} a^n = \infty, & a > 1 \end{array}

The function y(x) = e^x has two very important properties that make e an important number. First of all, y(x) = e^x is the only function for which the derivative of the function is a scalar multiple of itself.

\frac{d}{dx}e^{ax} = a\,e^{ax}

This is why e^{ax} is such a common part of the solutions to differential equations. Problems of growth and decay have solutions containing the number e.

Note

Do you see why the derivative of e^{a\,x} is a scalar multiple of itself? If we don’t use the known derivative of e^{a\,t}, we can either take the derivative of its Maclaurin (Taylor) series, or use it numeric definition in terms of a limit. I will use the later.

e^{a\,x} = \lim_{n\to\infty} \left(1 + \frac{a\,x}{n}\right)^n

You need to use the chain rule to take the derivative. If f(x) = \left(1 + \frac{a\,x}{n}\right)^n, then f'(x) = a\,\left(1 + \frac{a\,x}{n}\right)^{n - 1}. We see the desired equality then in the limit.

\begin{array}{rl} e^{a\,x} &= \lim_{n\to\infty} f(x) \\ \hfill \\ \frac{d\,}{dx}\left(e^{a\,x}\right) &= a\,\lim_{n\to\infty} f'(x) = a\,e^{a\,x} \end{array}

The second important property of e is defined by Euler’s formula.

11.12.3. Euler’s Formula

../_images/Leonhard_Euler.jpg

Fig. 11.3 Leonhard Euler (1707 - 1783)

Euler’s formula brings together complex numbers, the number e, and the trigonometry functions \cos and \sin into one equation.

e^{j\,\theta} = \cos(\theta) + j\,\sin(\theta)

Consider a point, C = a + j\,b, on the complex plane. Following Euler’s formula, C = r\,e^{j\,\theta} = r(\cos\,\theta + j\,\sin\,\theta)

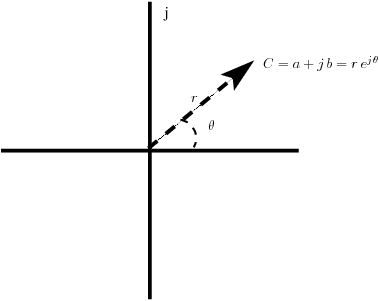
../_images/complex_pt.png

It can be shown, with the help of trigonometry identities, that powers of C follow the form expected from raising an exponential expression to a power.

C^n = r^n\,e^{j\,n\theta} = r^n(\cos\,n\theta + j\,\sin\,n\theta)

The needed trigonometry identities are:

\sin\,a\,\sin\,b = \frac{1}{2}(\cos(a-b) - \cos(a+b)) \\ \\ \cos\,a\,\cos\,b = \frac{1}{2}(\cos(a-b) + \cos(a+b)) \\ \\ \sin\,a\,\cos\,b = \frac{1}{2}(\sin(a-b) + \sin(a+b)) \\ \\

But it remains to shown that the number e is the base of the exponential.

Some MacLaurin series can show the validity of Euler’s formula.

\sin x = \sum_{n=0}^{\infty} \frac{(-1)^n\,x^{2n+1}}{(2n + 1)!} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots

\cos x = \sum_{n=0}^{\infty} \frac{(-1)^n\,x^{2n}}{(2n)!} = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots

e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots

Now replace x in the equations for e^x with jx. Remember that j^2 = -1.

\begin{array}{ll} e^{jx} & = 1 + jx + \frac{(jx)^2}{2!} + \frac{(jx)^3}{3!} + \frac{(jx)^4}{4!} + \frac{(jx)^5}{5!} + \frac{(jx)^6}{6!} + \frac{(jx)^7}{7!} + \ldots \\ & = 1 + jx - \frac{x^2}{2!} - \frac{jx^3}{3!} + \frac{x^4}{4!} + \frac{jx^5}{5!} - \frac{x^6}{6!} - \frac{jx^7}{7!} + \ldots \\ & = \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \right) + j \left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots \right) \\ & = \cos x + j \sin x \end{array}

The validity of Euler’s formula can also be show with a derivative and an integral.

Define z as:

z = \cos x + j \sin x

\frac{dz}{dx} = - \sin x + j \cos x

Now represent -1 as j^2.

\frac{dz}{dx} = j \cos x + j^2 \sin x = j\, (\cos x + j \sin x)

\frac{dz}{dx} = j\,z

\int \frac{1}{z}\, dz = \int j\, dx

\ln z = j\,x + C

Raise both sides to an exponent of e.

z = e^{j\,x} C

Letting x = 0 resolves the constant C to 1. Therefore,

z = e^{j\,x} = \cos x + j \sin x.

11.12.4. Numerical Proof Program

Write a C program that demonstrates the correctness of Euler’s formula for several values. Use the definition of e^x using a limit. A value of n = 1000, is sufficient for our purposes. Show numerically that when x = j\,\theta in the range 0 \leq \theta \leq \pi, the value of e^{j\,\theta} closely matches Euler’s formula.

The main code that you need to write is a function to compute exponential powers of a complex number. If one is already convinced of the correctness of Euler’s formula, then one can simplify complex exponentials by changing a complex number to polar coordinates and simply multiplying the angle. Since this program is intended to prove Euler’s formula, we should not take this short cut.

To make your program faster, use the recursive algorithm from Homework 8 - A Recursive Function to compute the exponential power.