12.4.8. Eigendecompostion from the Schur Triangular Form¶
The eigFrancis function handles the administrative
details of calculating eigenvalues and eigenvectors with the Francis
algorithm. It calls the schurFrancis function to find the
eigenvalues and the orthogonal component of the eigenvectors. The
eigenvectors are the product of the orthogonal Schur vectors and the
eigenvectors of the upper triangular matrix returned from the Schur
decomposition.
12.4.8.1. Eigenvalues of a Triangular Block Matrix¶
When the eigFrancis function is seeking only the eigenvalues of a
non-symmetric matrix, the ’real’ option is passed to the
schurFrancis function, which leaves nonzero values on the
subdiagonal where there is a 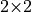 submatrix for a pair of
complex conjugate eigenvalues.
submatrix for a pair of
complex conjugate eigenvalues.
12.4.8.2. Eigenvalues of a triangular block matrix¶
Theorem 12.7 (Eigenvalues of a triangular block matrix)
Let matrix 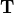 be a quasitriangular block matrix matrix
with at least one zero value on the subdiagonal. The set of
eigenvalues of
be a quasitriangular block matrix matrix
with at least one zero value on the subdiagonal. The set of
eigenvalues of 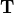 comprises the union of the eigenvalues
from its diagonal blocks. A zero value on the subdiagonal indicates a
division point of the blocks with a block above and to the left of
the zero and the other block to the right and below the zero. With
reference to equation (12.9),
comprises the union of the eigenvalues
from its diagonal blocks. A zero value on the subdiagonal indicates a
division point of the blocks with a block above and to the left of
the zero and the other block to the right and below the zero. With
reference to equation (12.9),
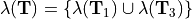 .
.
(12.9)¶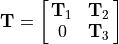
As illustrated below, A quasitriangular matrix may be split into
blocks based on zero and nonzero values on the subdiagonal.
The eigenvalues of the by{2}{2} submatrix holding
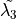 and
and 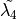 are needed
to find
are needed
to find 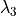 and
and 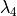 .
.
Proof. Since the eigenvalues are the roots of the characteristic equation
given by 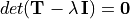 , we
look at how determinants of block-diagonal matrices are calculated to
gain the form of the characteristic polynomial. First, establish the
determinant of matrix products,
, we
look at how determinants of block-diagonal matrices are calculated to
gain the form of the characteristic polynomial. First, establish the
determinant of matrix products, 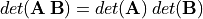 . Next, consider block diagonal
matrices with an identity matrix, which flows from Laplace expansion
and that
. Next, consider block diagonal
matrices with an identity matrix, which flows from Laplace expansion
and that 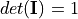 .
.
(12.10)¶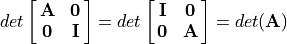
Now express equation (12.9) as a product of matrices.
(12.11)¶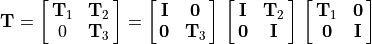
The determinant of the middle matrix of equation
(12.11) is one because it is upper triangular with ones
on the diagonal. From
equation (12.10), the determinant of equation
(12.11) is
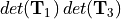 . By applying these
determinants to characteristic equations, we get a product of
polynomials from
. By applying these
determinants to characteristic equations, we get a product of
polynomials from 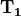 and
and 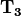 equating to a
union of eigenvalues.
equating to a
union of eigenvalues.

The conclusion of Eigenvalues of a triangular block matrix is that a zero on the
subdiagonal of a matrix in Hessenberg form means that we may split the
matrix at that point. The code in eigFrancis takes advantage of
this. When a zero is found on the subdiagonal, the block of elements
above the zero is closed, and a new block is started with the elements
to the right and below the zero. Consecutive zeros will close and start
new blocks after each diagonal so that each diagonal element is an
eigenvalue. A nonzero element extends the current block. Then
eigFrancis is called recursively for each
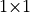 and
and 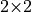 submatrix, which finds the
eigenvalues of the small blocks from direct calculations.
submatrix, which finds the
eigenvalues of the small blocks from direct calculations.
12.4.8.3. The eigFrancis Function¶
function [X, Lambda] = eigFrancis(A)
% EIGFRANCIS - Find the eigenvalues and eigenvectors of a matrix using
% Francis's algorithm, a.k.a. implicitly-shifted QR.
%
% A - Square matrix
% EIGFRANCIS(A) or L = EIGFRANCIS(A) returns the eigenvalues of A.
% [X, L] = EIGFRANCIS(A) returns the eigenvectors of A as the columns
% of the X matrix and the eigenvalues of A are along the diagonal
% of matrix L.
%
% The degree two Francis algorithm is used in finding complex
% eigenvalues. The degree one algorithm does everything else.
%
% This function does some housekeeping and calls other functions to
% implement the algorithms.
%
% NOTE: This code is for educational purposes.
% For other purposes, use MATLAB's eig function.
%
% see also: EIG, EIG22, HESS, SCHURFRANCIS, UTEIGVECT
[m, n] = size(A);
if m ~= n
error("Matrix must be square to find eigenvalues")
end
if m == 1, if nargout <= 1, X = A; else, X = 1; Lambda = A; end
return, end
if m == 2
[l1, l2] = eig22(A);
if nargout > 1
Lambda = diag([l1 l2]);
X = [null(A - l1*eye(2)), null(A - l2*eye(2))];
else, X = [l1; l2];
end, return
end
tol = 1e-14;
if nargout <= 1 % only want eigenvalues
B = hess(A);
% Split if any zeros are on the subdiagonal
for k = 1:n-1
if abs(B(k+1,k)) < tol
L1 = eigFrancis(B(1:k,1:k));
L2 = eigFrancis(B(k+1:m,k+1:n));
X = [L1; L2];
return;
end % Any other zeros found in recursion.
end
if isequal(A, A') % Hermitian symmetric
L = schurFrancis(B, 'real');
else
L = schurFrancis(B);
end
X = diag(L);
return
else % Find eigenvectors also
if isequal(A, A') % Hermitian symmetric
% Schur decomposition = eigendecomposition
[X, L] = schurFrancis(A, 'real');
else
[Q, L] = schurFrancis(A); % L is upper triangular
V = UTeigVect(L);
X = Q*V;
for k=1:n % no round-off on imag of real numbers
if abs(imag(L(k,k))) < tol
X(:,k) = real(X(:,k));
L(k,k) = real(L(k,k));
end
end
end
Lambda = L.*eye(n); % zeros except on diagonal
end
end
