11.3. Homework 3 - Control Constructs and Newton’s Square Root Algorithm

In class, we discussed an algorithm developed by Sir Isaac Newton to find the square root of a number using an iterative approximation algorithm. We worked an example of how to implement the algorithm using a for loop. For this assignment, you should replace the for loop with a while loop, which determines if the result after each loop iteration is close enough to the square root of K. Note that there are multiple ways to determine this. You could square the result and compare it to K. You could also check for convergence of the result because once the \sqrt{K} is found, further loop iterations will not change the result.

Report how many times the loop executed to calculate the answer.

Numeric Roots of a Function Algorithm

The algorithm for finding the square root of a number is actually an instance of an algorithm for finding a root of a function (x for which f(x) = 0).

The Newton-Raphson method, or just Newton’s method, uses lines that are tangent to the curve of a function to estimate where the function crosses the x-axis.

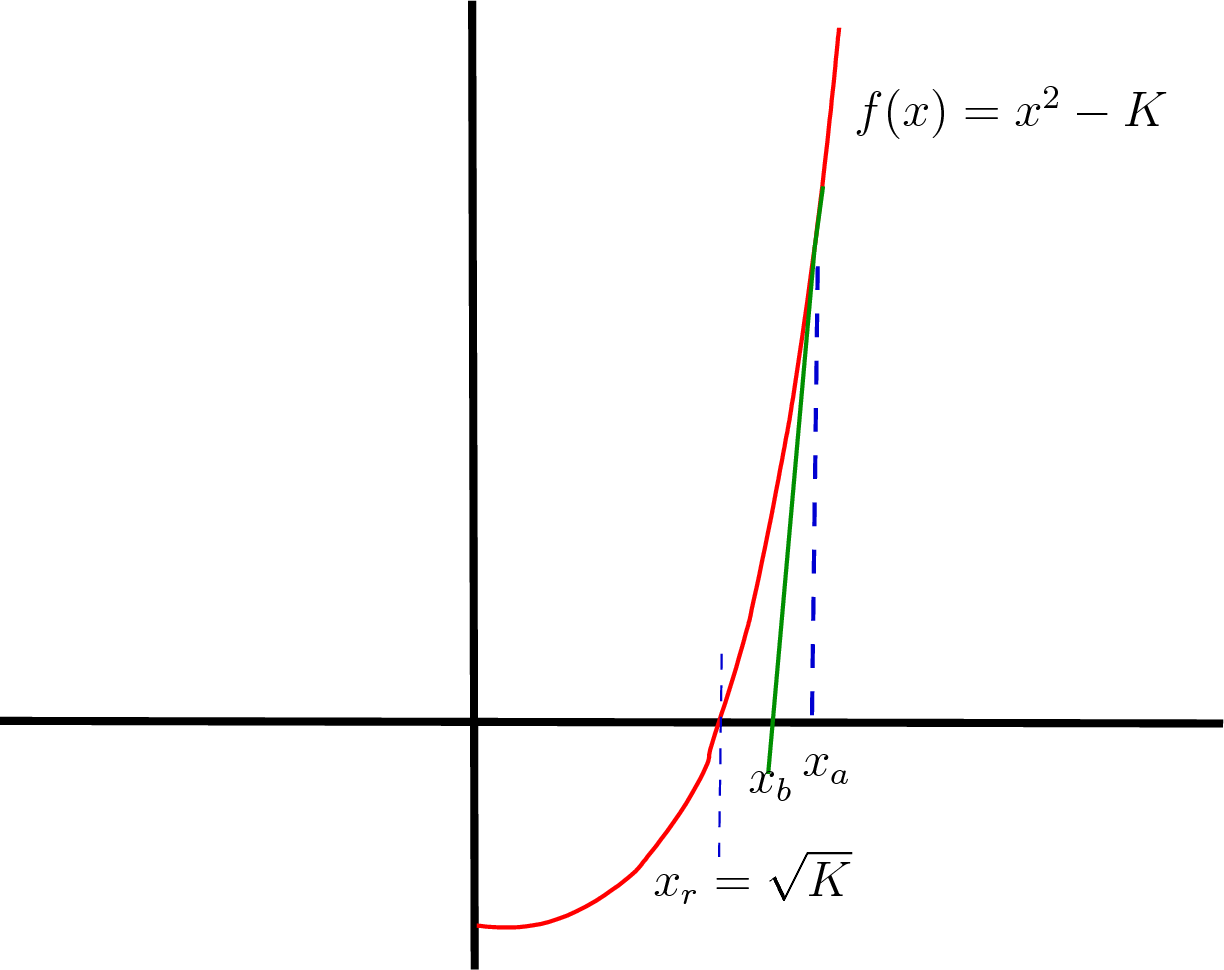
../_images/newton.png

Fig. 11.1 The Newton-Raphson method extends a tangent line to the x-axis to estimate of a root and repeats the process until the root is found with an allowed tolerance.

The algorithm evaluates the function at a sequence of estimates until the root is found.

  1. Evaluate the function and its derivative at the first estimate, f(x_a) and f'(x_a).

  2. The equation for a tangent line passing through the x-axis is

    0 = f(x_a) - f'(x_a)(x_b - x_a).

  3. The estimate for the root is then

    x_b = x_a - \frac{f(x_a)}{f'(x_a)}.

  4. If x_b is not close enough to the root, let x_a = x_b and repeat the steps.

The above graph shows a function for finding \sqrt{K}. Let f(x) = x^2 - K, then f'(x) = 2\,x.

\begin{array}{rl} x_b &= x_a - \frac{(x_a^2 - K)}{2\,x_a} \\ &= \frac{x_a + \frac{K}{x_a}}{2} \end{array}

Newton’s Square Root Algorithm

For any K > 0, we wish to calculate the exact value or a close approximation to \sqrt{K}.

Begin with any x_a, 0 < x_a \leq K. We define the next approximation to \sqrt{K}, x_b, as:

x_b = \frac{x_a + \frac{K}{x_a}}{2}

If we define the errors between the actual square root of K and x_a and x_b as \delta and \epsilon,

\delta = | \sqrt{K} - x_a |

\epsilon = | \sqrt{K} - x_b |

then Newton’s Square Root Algorithm claims that:

0 \leq \epsilon \leq \delta

That is either, x_a = x_b = \sqrt{K} or x_b is closer to the value of \sqrt{K} than is x_a.

If \bm{x_a = \sqrt{K}} :

\frac{K}{x_a} = \frac{K}{\sqrt{K}} = \sqrt{K}

and x_b = x_a.

If \bm{x_a > \sqrt{K}} :

\frac{K}{x_a} < \sqrt{K}

and x_b, which is the average of x_a and \frac{K}{x_a}, will be greater than x_a and thus closer to \sqrt{K} than x_a.

If \bm{x_a < \sqrt{K}} :

\frac{K}{x_a} > \sqrt{K}

and x_b, which is the average of x_a and \frac{K}{x_a}, will be less than x_a and thus closer to \sqrt{K} than x_a.

It follows then that a loop may be constructed to approximate \sqrt{K}:

x_a = x/2;
loop:
    x_b = (x_a + K/x_a)/2;
    x_a = x_b;

The matter of how many times to execute this loop is the primary concern of this homework assignment.